|
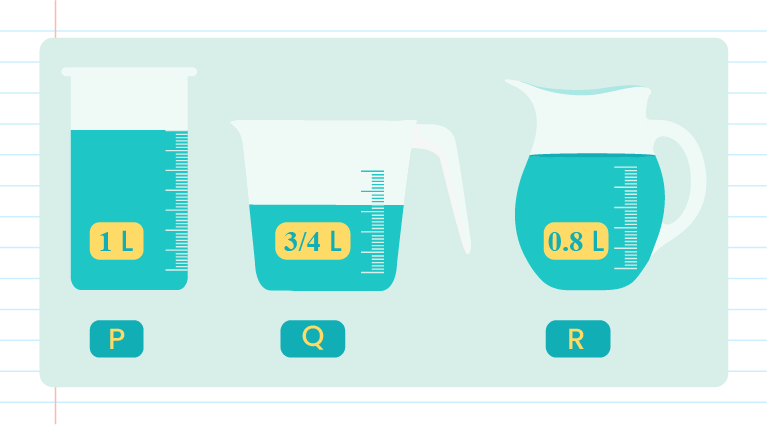
The volume of the three water containers P, Q and R is as shown in the picture. How much more is the volume of water, in \(\ell\), in containers P and Q compared to container R?
MATHEMATICAL SENTENCE:
\(1\,\ell\;+\;\dfrac{3}{4}\,\ell\;-\;0\,.\,8\,\ell=\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}\)
STEP 1:
\(\dfrac{3}{4}=0.75\)
STEP 2:
\(\begin{array} {rr} \quad \\1\;.\;\color{red}{0}\;\color{red}{0} \\+\quad0\;.\;7\;5 \\\hline\quad1\;.\;7\;5 \\\hline \end{array}\)
STEP 3:
\(\begin{array} {rr} \small{\color{red}{0}}\quad\small{\color{red}{17}}\;\; \\\cancel{1}\;.\;\cancel{7}\;5 \\-\quad0\;.\;8\;\color{red}{0} \\\hline\quad0\;.\;9\;5 \\\hline \end{array}\)
\(1\,\ell\;+\;\dfrac{3}{4}\,\ell\;-\;0\,.\,8\,\ell=0.95\,\ell\)
|
\(0.8=\dfrac{8}{10}\;\ell\)
\(1+\dfrac{3}{4}-0.8\\\,\\=1+\dfrac{3\times\color{red}5}{4\times\color{red}5}-\dfrac{8\times\color{red}2}{10\times\color{red}2}\\\,\\=\dfrac{20}{20}+\dfrac{15}{20}-\dfrac{16}{20}\\\,\\=\dfrac{35}{20}-\dfrac{16}{20}\\\,\\=\dfrac{19}{20}\)
\(1\,\ell\;+\;\dfrac{3}{4}\,\ell\;-\;0\,.\,8\,\ell=\dfrac{19}{20}\,\ell\)
|
CONCLUSION:
\(1\,\ell\;+\;\dfrac{3}{4}\,\ell\;-\;0\,.\,8\,\ell=0.95\,\ell\) or \(\dfrac{19}{20}\,\ell\).
The volume of water in containers P and Q is more than \(0.95\,\ell\) or \(\dfrac{19}{20}\,\ell\) more than in container R.
|
|
|
| MULTIPLICATION & DIVISION |
Robot P has a height of \(0.75\) m. The height of robot P is 3 times the height of robot Q, while the height of robot R is \(\dfrac{1}{2}\) of the height of robot Q. What is the height of robot R?
MATHEMATICAL SENTENCE:
\(0.75\space\text{m}\space\div\;3\;\times\;\dfrac{1}{2}=\underline{\ \ \ \ \ \ \ \ \ \ }\text{ m}\)
STEP 1:
\(\;\;\;\;0.25\;\;\\3\overline{\smash{)}\;0.75}\; \\\,\underline{-\;0} \\\;\;\;\,\;0\ 7 \\\;\;\underline{-\;\;6}\ \\\ \;\;\;\;\;\,\;15 \\\;\;\;\;\,\underline{-15}\ \ \\\ \;\;\;\;\;\;\;\;\,0\)
STEP 2:
\(0.25\times\dfrac{1}{2}=0.125\)
CONCLUSION:
The height of robot R is 0.125 m.
|
| ADDITION & MULTIPLICATION |
\(16\times(5.5+3\dfrac{1}{4})=\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}\)
TIPS: Complete the operations in parentheses first.
STEP 1:
\(\quad5.5\\\,\\=5\dfrac{5\div5}{10\div5}\\\,\\=5\dfrac{1}{2}\)
STEP 2:
\(\;\;\;\;5.5+3\dfrac{1}{4}\\\,\\=5\dfrac{1\times2}{2\times2}+3\dfrac{1}{4}\\\,\\=5\dfrac{2}{4}+3\dfrac{1}{4}\\\,\\=8\dfrac{3}{4}\)
STEP 3:
\(\quad16\times8\dfrac{3}{4}\\\,\\=16\times\dfrac{35}{4}\\\,\\=140\)
|
| SUBTRACTION & MULTIPLICATION |
\((9.2-7)\times(\dfrac{4}{5}-0.6)=\underline{ }\underline{ }\underline{ }\underline{ }\underline{ }\underline{ }\underline{ }\)
STEP 1:
\(\begin{array} {rr} 9\;.\;2 \\-\quad7\;.\;\color{red}{0} \\\hline\quad2\;.\;2 \\\hline \end{array}\)
STEP 2:
\(\quad\dfrac{4\times2}{5\times2}\\\,\\=\dfrac{8}{10}\\\,\\=0.8\)
\(0.8-0.6=0.2\)
STEP 3:
\(\begin{array} {rr} 2\;.\;2 \\\times\quad0\;.\;2 \\\hline\quad4\;\;\;\,4 \\+\quad0\;\;0\;\;\;\color{blue}{0} \\\hline0\,.\,4\;\;\;4 \\\hline \end{array}\)
CONCLUSION:
\((9.2-7)\times(\frac{4}{5}-0.6)=0.44\)
|
|
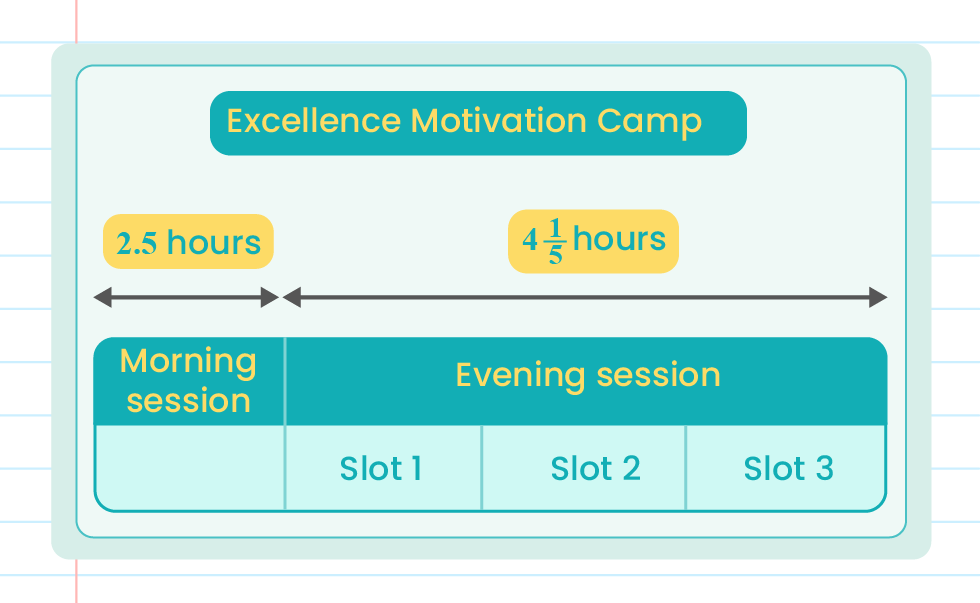
Calculate the total duration for the morning session and the first slot of the afternoon session based on the diagram.
MATHEMATICAL SENTENCE:
\(2.5\text{ hours}+4\dfrac{1}{5}\text{ hours}\div3=\underline{ }\underline{}\underline{}\underline{}\underline{}\underline{}\underline{}\)
STEP 1:
\(\quad4\dfrac{1}{5}\div3\\=4.2\div3\\=1.4\)
STEP 2:
\(2.5+1.4=3.9\)
STEP 1:
\(\quad4\dfrac{1}{5}\div3\\\,\\=\dfrac{21}{5}\div\dfrac{3}{1}\\\,\\=\dfrac{21}{5}\times\dfrac{1}{3}\\\,\\=\dfrac{7}{5}\\\,\\=1\dfrac{2}{5}\)
STEP 2:
\(1\dfrac{1}{2}=1.4\)
\(2.5+1.4=3.9\)
|
CONCLUSION:
\(2.5\text{ hours}+4\dfrac{1}{5}\text{ hours}\div3=3.9\text{ hours}\)
The total duration of the morning session and the first slot of the afternoon session is 3.9 hours.
|
\(2.25\text{ hours}-3\dfrac{1}{2}\text{ hours}\div4=\underline{}\underline{\,\,\,\,\,\,\,\,\,\,}\text{ hours}\)
STEP 1:
\(\quad3\dfrac{1}{2}\div4\\\,\\=\dfrac{7}{2}\div\dfrac{4}{1}\\\,\\=\dfrac{7}{2}\times\dfrac{1}{4}\\\,\\=\dfrac{7}{8}\)
STEP 2:
Convert 2.25 to fraction.
\(\quad2.25\\\,\\=2\dfrac{25\div25}{100\div25}\\\,\\=2\dfrac{1}{4}\\\,\\=\dfrac{9}{4}\)
STEP 3:
\(\quad\dfrac{9\times2}{4\times2}-\dfrac{7}{8}\\\,\\=\dfrac{18}{8}-\dfrac{7}{8}\\\,\\=\dfrac{11}{8}\\\,\\=1\dfrac{3}{8}\)
|