| |
| 2.1 |
Multiplication of Fractions |
Multiply proper fractions with proper fractions
- Multiply the numerator with the numerator.
- Multiply the denominator with the denominator.
- Give the answer in the simplest form.
| Question |
|
Fraction Multiplication
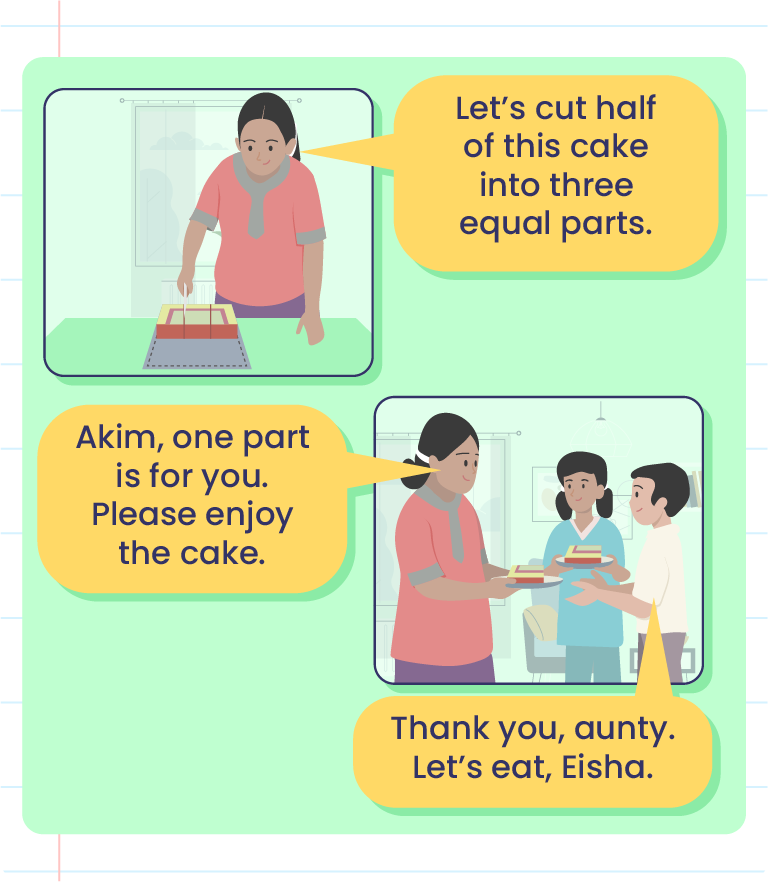 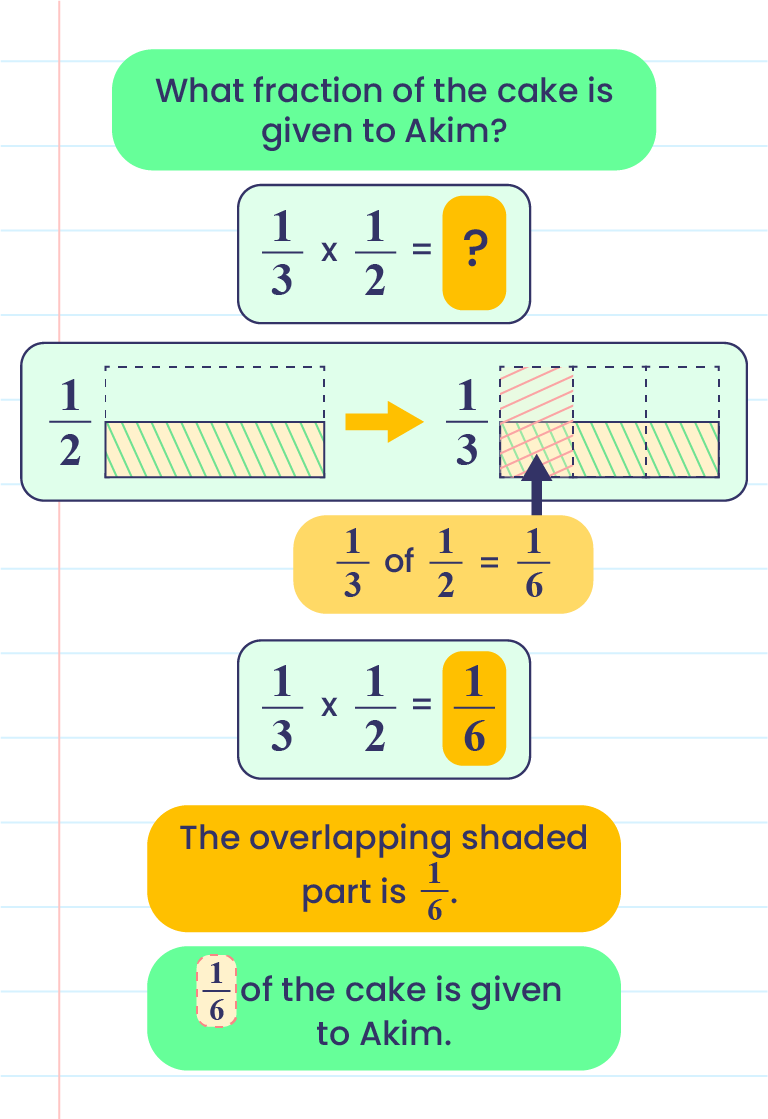 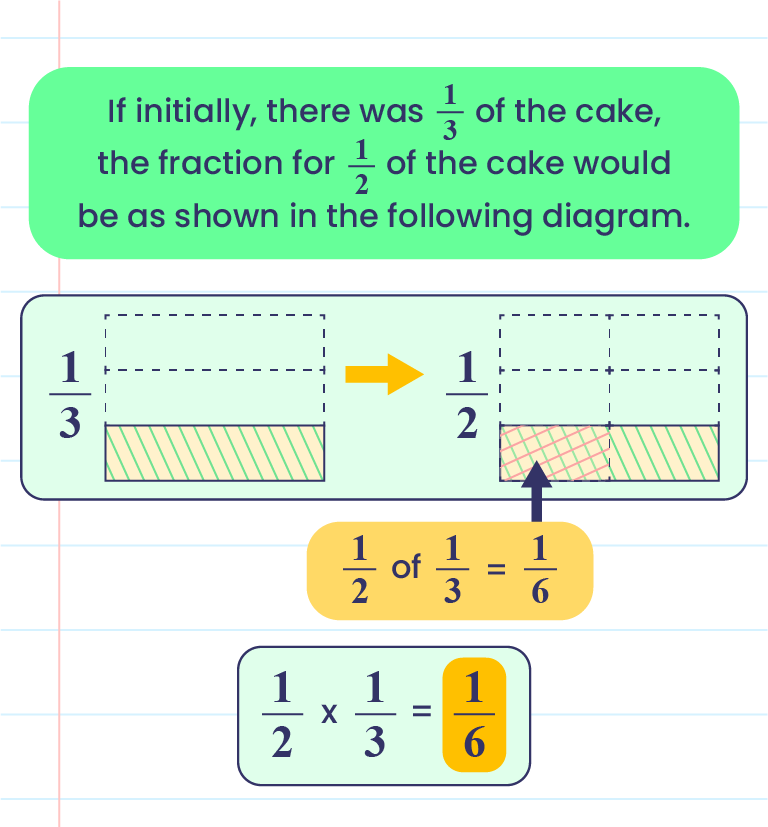 
|
|
Shading Method
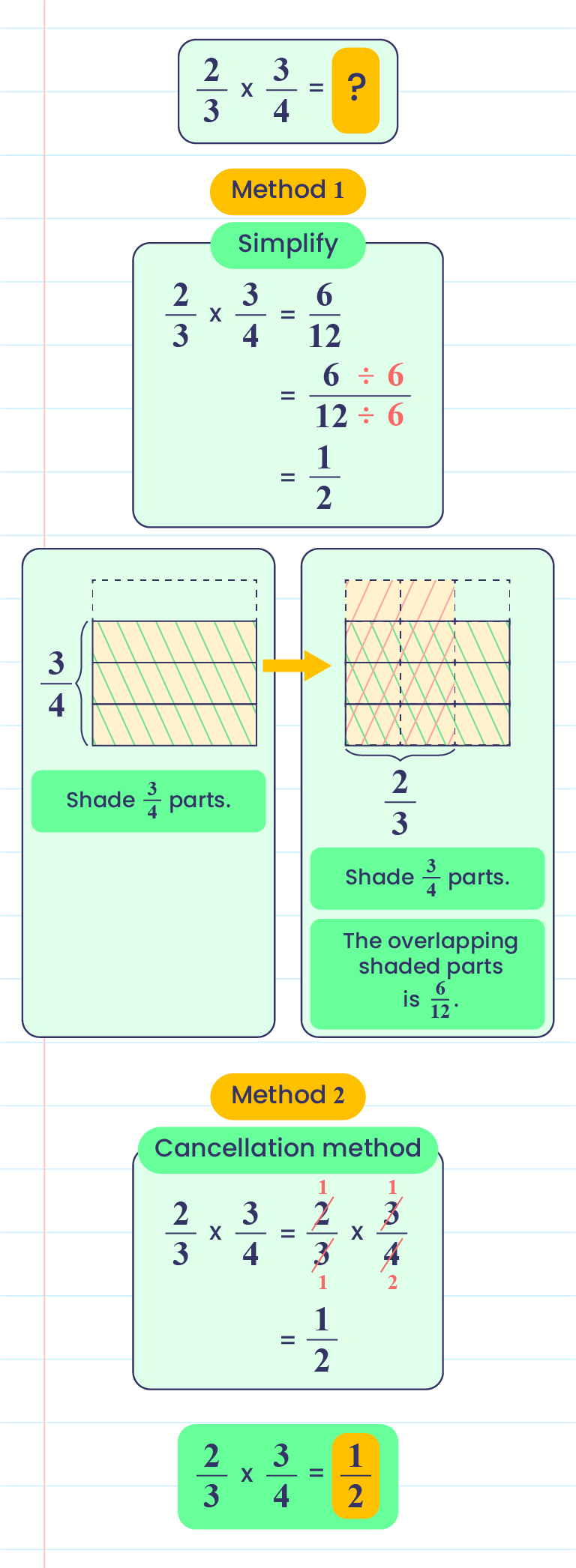 
|
|
Cancellation Method
\(\begin {array} {rr} \\ \quad\quad\small{\color{red}1}\quad\quad\small{\color{red}1} \\ \dfrac{2}{3}\times\dfrac{3}{4}=\dfrac{\cancel2}{\cancel3}\times\dfrac{\cancel3}{\cancel4}\\ \quad\quad\small{\color{red}1}\quad\quad\small{\color{red}1}\\ = \dfrac{1}{2}\quad\quad \end {array}\)

|
|
Steps to Multiply the Numerators and the Denominators
\(\dfrac{3}{5}\times\dfrac{2}{7}=\dfrac{3\times2}{5\times7}\\ \quad\quad\quad\quad\quad =\dfrac{6}{35} \)
|
|
|
Multiply proper fractions with mixed numbers
Situation 1
Mr Leong has \(3\dfrac{1}{2}\) packets of fertilizer. He wants to use \(\dfrac{2}{5}\)of the fertilizer to fertilize his hibiscus plant. How many packets of the fertilizer will he use to fertilize the hibiscus plant?
\(\dfrac{2}{5}\times3\dfrac{1}{2}=\dfrac{2}{5}\times\dfrac{7}{2}\\ \quad\quad\quad\quad=\dfrac{14}{10}\\ \quad\quad\quad\quad=1\dfrac{4\div2}{10\div2}\\ \quad\quad\quad\quad=1\dfrac{2}{5} \) 
|
| |
|
Multiply mixed numbers with mixed numbers
- A fraction multiplied by the inverse of the fraction will give the answer 1.
|
|
Situation 1
\(1\dfrac{1}{3}\times1\dfrac{1}{2}= \)
\(1\dfrac{1}{3}\times1\dfrac{1}{2}=(1\times1\dfrac{1}{2})+(\dfrac{1}{3}\times1\dfrac{1}{2})\\ \quad\quad\quad\quad=1\dfrac{1}{2}+(\dfrac{1}{3}\times\dfrac{3}{2})\\ \quad\quad\quad\quad=1\dfrac{1}{2}+\dfrac{3\div3}{6\div3}\\ \quad\quad\quad\quad=1\dfrac{1}{2}+\dfrac{1}{2}\\ \quad\quad\quad\quad=2 \) 
|
|
|
| |
| 2.2 |
Division of Fractions |
Divide proper fractions by whole numbers
|
|
Situation 1
\(\begin {array} {rr}\\ \dfrac{4}{5}\div8=\dfrac{4}{5}\div\dfrac{8}{1}\quad\quad\quad\quad\quad\\ \quad\small{\color{red}1}\quad\quad\quad\quad\quad\quad\quad\quad\\ =\dfrac{\cancel4}{5}\times\dfrac{1}{\cancel8}\quad\quad\quad\quad\quad\\ \quad\quad\quad\small{\color{red}2}\quad\quad\quad\quad\quad\\ \quad=\dfrac{1}{5}\times\dfrac{1}{2}\quad\quad\quad\quad\quad\\ \quad=\dfrac{1}{10}\quad\quad\quad\quad\quad\quad \end {array} \) 
|
|

|
|
Divide proper fractions by proper fractions
- Change division to multiplication.
- Inverse the divisor.
- Simplify the numerator and the denominator by cancellation (if any).
|
|
Situation 1
This is only \(\dfrac{3}{4}\)m. Cut the wood into a few pieces, each measuring \(\dfrac{1}{8}\)m. How many pieces of wood measuring \(\dfrac{1}{8}\)m were cut by Paramjit's father?
\(\dfrac{3}{4} m\div\dfrac{1}{8}m=\)
\(\quad\quad\quad\quad\quad\quad\small{\color{red}2}\\ \dfrac{3}{4}\div\dfrac{1}{8}=\dfrac{3}{\cancel4}\times\dfrac{\cancel8}{1}\\ \quad\quad\quad\quad\quad\small{\color{red}1}\\ \quad\quad\quad=6\) 
|
|

|
|
Divide mixed numbers by whole numbers
|
|
Situation 1
\(1\dfrac{7}{9}\div4=\\ 1\dfrac{7}{9}\div4=1\dfrac{7}{9}\div\dfrac{4}{1}\\ \quad\quad\quad\quad\small{\color{red}4}\\ \quad\quad\quad=\dfrac{\cancel{16}}{9}\times\dfrac{1}{\cancel4}\\ \quad\quad\quad\quad\quad\quad\quad\small{\color{red}1}\\ \quad\quad\quad=\dfrac{4}{9} \) 
|
|
Situation 2
\(6\dfrac{2}{7}\div22=\\ 6\dfrac{2}{7}\div22=6\dfrac{2}{7}\div\dfrac{22}{1}\\ \quad\quad\quad\quad\small{\color{red}2}\\ \quad\quad\quad=\dfrac{\cancel{44}}{7}\times\dfrac{1}{\cancel{22}}\\ \quad\quad\quad\quad\quad\quad\quad\small{\color{red}1}\\ \quad\quad\quad=\dfrac{2}{7} \) 
|
|
Divide mixed numbers by proper fractions
|
|
Situation 1
How many \(\dfrac{1}{5}\)are there in \(1\dfrac{1}{2}\)?
\(1\dfrac{1}{2}\div\dfrac{1}{5}=\dfrac{3}{2}\times\dfrac{5}{1}\\ \quad\quad\quad=\dfrac{15}{2}\\ \quad\quad\quad=7\dfrac{1}{2} \) 
|
|
|
|
Situation 1
The recipe to make chocolate chip muffins is as shown. \(\dfrac{3}{4}\)cup of chocolate chips is needed to produce 12 muffins. Zara tried the recipe and used only half of the flour. How chocolate chips did Zara use?
| A Recipe for Chocolate Chip Muffins (12 pieces) |
|
2 cups of flour
1/2 cup of granulated sugar
3 teaspoons of baking powder
1/2 teaspoon of milk
1/3 cup od cooking oil
1 egg
3/4 cup of chocolate chips
3 tablespoons of white sugar
2 tablespoons of brown sugar
|

|
|
Solution
\(\dfrac{1}{2}\times\dfrac{3}{4}=\dfrac{1\times3}{2\times4}\\ \quad\quad\quad=\dfrac{3}{8}\)
|
|
Situation 2
Damia has \(1\dfrac{1}{2} m\) of ribbon. She uses \(\dfrac{1}{3}\)of the ribbon to decorate her mother's gift box. What is the length of the ribbon that she uses?

|
|
Solution
\(\quad\quad\quad\quad\quad\quad\small{\color{red}1}\\ \dfrac{1}{3}\times1\dfrac{1}{2}=\dfrac{1}{\cancel3}\times\dfrac{\cancel3}{2}\\ \quad\quad\quad\quad\quad\small{\color{red}1}\\ \quad\quad\quad\quad=\dfrac{1}{1}\times\dfrac{1}{2}\\ \quad\quad\quad\quad=\dfrac{1}{2}\)
|