| |
|
6.1
|
The Value of Sine, Cosine and Tangent for Angle \(\theta, 0^\circ \leq θ \leq 360^\circ\)
|
|
| |
| What is corresponding reference angle? |
| |
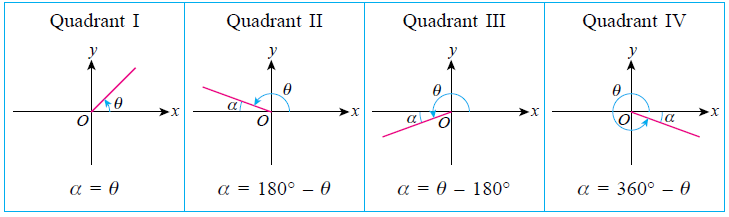
| The corresponding reference angle, \(\alpha\), is always less than \(90^\circ\). Angles in quadrants II, III and IV have corresponding reference angles, . The angle in quadrant I itself is the corresponding reference angle, \(\alpha=\theta\). |
| |
 |
| |
| The reference angles in quadrants II, III and IV are the corresponding angles in quadrant I. |
| |
|
|
| |
| Example 1 |
| |
| Determine the quadrant and the corresponding reference angle for each of the following. |
| a) \(138^\circ \) (b) \(239^\circ \) c) \(312^\circ\) |
| |
| Solution: |
| |
| \(\begin{aligned} \text{a)}\hspace{1mm}&\text{$138^\circ$ is located in quadrant II.}\\ &\text{Corresponding reference angle, } \alpha\\ &= 180^\circ - 138^\circ\\ &= 42^\circ \end{aligned}\) |
| |
| \(\begin{aligned} \text{b)}\hspace{1mm}&\text{$239^\circ$ is located in quadrant III.}\\ &\text{Corresponding reference angle, } \alpha\\ &= 239^\circ - 180^\circ\\ &= 59^\circ \end{aligned}\) |
| |
| \(\begin{aligned} \text{c)}\hspace{1mm}&\text{$312^\circ$ is located in quadrant IV.}\\ &\text{Corresponding reference angle, } \alpha\\ &= 360^\circ - 312^\circ\\ &= 48^\circ \end{aligned}\) |
| |
|
|
| |
| The relationship between the function of sine, cosine and tangent for angles in quadrants II, III and IV with the corresponding reference angle |
| |
| Quadrant II |
\(\begin{aligned} &\sin \theta = + \sin \alpha = + \sin (180^\circ - \theta)\\ &\cos \theta = - \cos \alpha= - \cos (180^\circ - \theta)\\ &\tan \theta = - \tan \alpha = - \tan (180^\circ - \theta) \end{aligned}\) 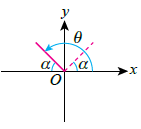 |
| |
| Quadrant III |
\(\begin{aligned} &\sin \theta = - \sin \alpha = -\sin ( \theta-180^\circ)\\ &\cos \theta = - \cos \alpha= - \cos (\theta-180^\circ)\\ &\tan \theta = - \tan \alpha = +\tan (\theta-80^\circ) \end{aligned}\) 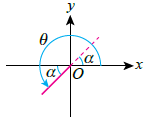 |
| |
| Quadrant IV |
\(\begin{aligned} &\sin \theta = - \sin \alpha = -\sin ( 360^\circ-\theta)\\ &\cos \theta = + \cos \alpha= + \cos (360^\circ-\theta)\\ &\tan \theta = - \tan \alpha = -\tan (360^\circ-\theta) \end{aligned}\) 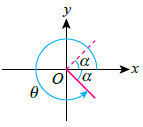 |
| |
| In summary: |
| |
 |
| |
|
|
| |
| What is a unit circle? |
| |
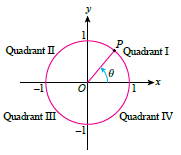
| The diagram below shows a unit circle. A unit circle is a circle that has a radius of 1 unit and is centered on the origin. The \(x\)-axis and -axis divide the unit circle into 4 equal quadrants, namely quadrant I, quadrant II, quadrant III and quadrant IV. |
| |
 |
| |
| It is given that P is a point that moves along the circumference of the unit circle and q is the angle formed by the radius of the unit circle, OP, from the positive x-axis in an anticlockwise direction. It is found that |
(a) point P is in quadrant I when\(0^\circ\lt\theta\lt90^\circ\),
(b) point P is in quadrant II when \(90^\circ\lt\theta\lt180^\circ\),
(c) point P is in quadrant III when \(180^\circ\lt\theta\lt270^\circ\),
(d) point P is in quadrant IV when \(270^\circ\lt\theta\lt360^\circ\). |
| |
|
|
| |
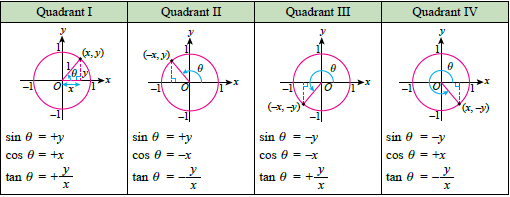
| Relationship between the values of sine, cosine and tangent with the values of x-coordinate and y-coordinate for angles in quadrants II, III and IV in a unit circle. |
| |
 |
| |
|
|
| |
| Example 2 |
| |
| The following diagram shows a unit circle and angle \(\theta\). Determine the values of \(\sin \theta, \cos \theta\hspace{1mm}\text{and}\hspace{1mm} \tan \theta\). |
| |
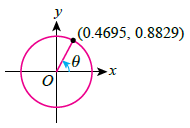 |
| |
| Solution: |
| |
| \(\begin{aligned} \sin \theta &= 0.8829\\ \cos \theta &= 0.4695\\ \tan \theta&=\frac{0.8829}{ 0.4695}\\ &=1 .8805 \end{aligned}\) |
| |
|
|
| |
| The value of sine, cosine and tangent at angles \(30^\circ, 45^\circ\text{ and } 60^\circ\) |
| |
| |
\(30^\circ\) |
\(60^\circ\) |
\(45^\circ\) |
| \(\sin \theta\) |
\(\begin{aligned} 1\over 2 \end{aligned}\) |
\(\begin{aligned} \sqrt{3}\over 2 \end{aligned}\) |
\(\begin{aligned} 1\over \sqrt{2} \end{aligned}\) |
| \(\cos \theta\) |
\(\begin{aligned} \sqrt{3}\over 2 \end{aligned}\) |
\(\begin{aligned} 1\over 2 \end{aligned}\) |
\(\begin{aligned} 1\over \sqrt{2} \end{aligned}\) |
| \(\tan \theta\) |
\(\begin{aligned} 1\over \sqrt{3} \end{aligned}\) |
\(\begin{aligned} \sqrt{3} \end{aligned}\) |
\(\begin{aligned} 1 \end{aligned}\) |
|
| |
|
|
| |
| Example 3 |
| |
| Without using a scientific calculator, determine the value for each of the following based on the corresponding reference angle. |
| a) \(\cos 150^\circ\) b) \(\tan 225^\circ\) (c) \(\sin300^\circ\) |
| |
| Solution: |
| |
| \(\begin{aligned} \text{a) }\cos 150^\circ&=-\cos(180^\circ-150^\circ)\\ &=-\cos30^\circ\\ &=-\frac{\sqrt{3}}{2} \end{aligned}\) |
| |
| \(\begin{aligned} \text{b) }\tan 225^\circ&=+\tan(225^\circ-180^\circ)\\ &=+\tan45^\circ\\ &=1 \end{aligned}\) |
| |
| \(\begin{aligned} \text{c) }\sin 300^\circ&=-\sin(260^\circ-300^\circ)\\ &=-\sin60^\circ\\ &=-\frac{\sqrt{3}}{2} \end{aligned}\) |
| |
|
|
| |
| Example 4 |
| |
| a) Given that \(\sin \theta=0.6157 \text{ and }0^\circ\leq\theta\leq360^\circ\), calculate the angle \(\theta\). |
| b) Given that \(\cos \theta=-0.4226 \text{ and }0^\circ\leq\theta\leq360^\circ\) calculate the angle \(\theta\). |
| c) Given that \(\tan \theta=-1.4826 \text{ and }0^\circ\leq\theta\leq60^\circ\) calculate the angle \(\theta\). |
| |
| Solution: |
| |
| \(\begin{aligned} \text{a) }&\sin \theta =0.6157 \text{(+ sign}\implies \text{quadrant I or II}) \\ &\text{Corresponding angle}\\ &=\sin^{-1}0.6157\\ &=38^\circ.\\ &\therefore\theta=38^\circ \text{ or } 142^\circ \end{aligned}\) |
| |
| \(\begin{aligned} \text{b) }&\cos \theta =-0.4226 \text{(- sign}\implies \text{quadrant II or III}) \\ &\text{Corresponding angle}\\ &=\cos^{-1}-0.4226\\ &=65^\circ.\\ &\therefore\theta=115^\circ \text{ or } 245^\circ \end{aligned}\) |
| |
| \(\begin{aligned} \text{c) }&\tan \theta =-1.4826 \text{(- sign}\implies \text{quadrant II or IV}) \\ &\text{Corresponding angle}\\ &=\tan^{-1}-1.4826\\ &=56^\circ.\\ &\therefore\theta=124^\circ \text{ or } 304^\circ \end{aligned}\) |
| |
|
|
| |
| |