| 8.1 |
Displacement, Velocity and Acceleration as a Function of Time |
|
| |
 |
| |
| Displacement and Distance |
|
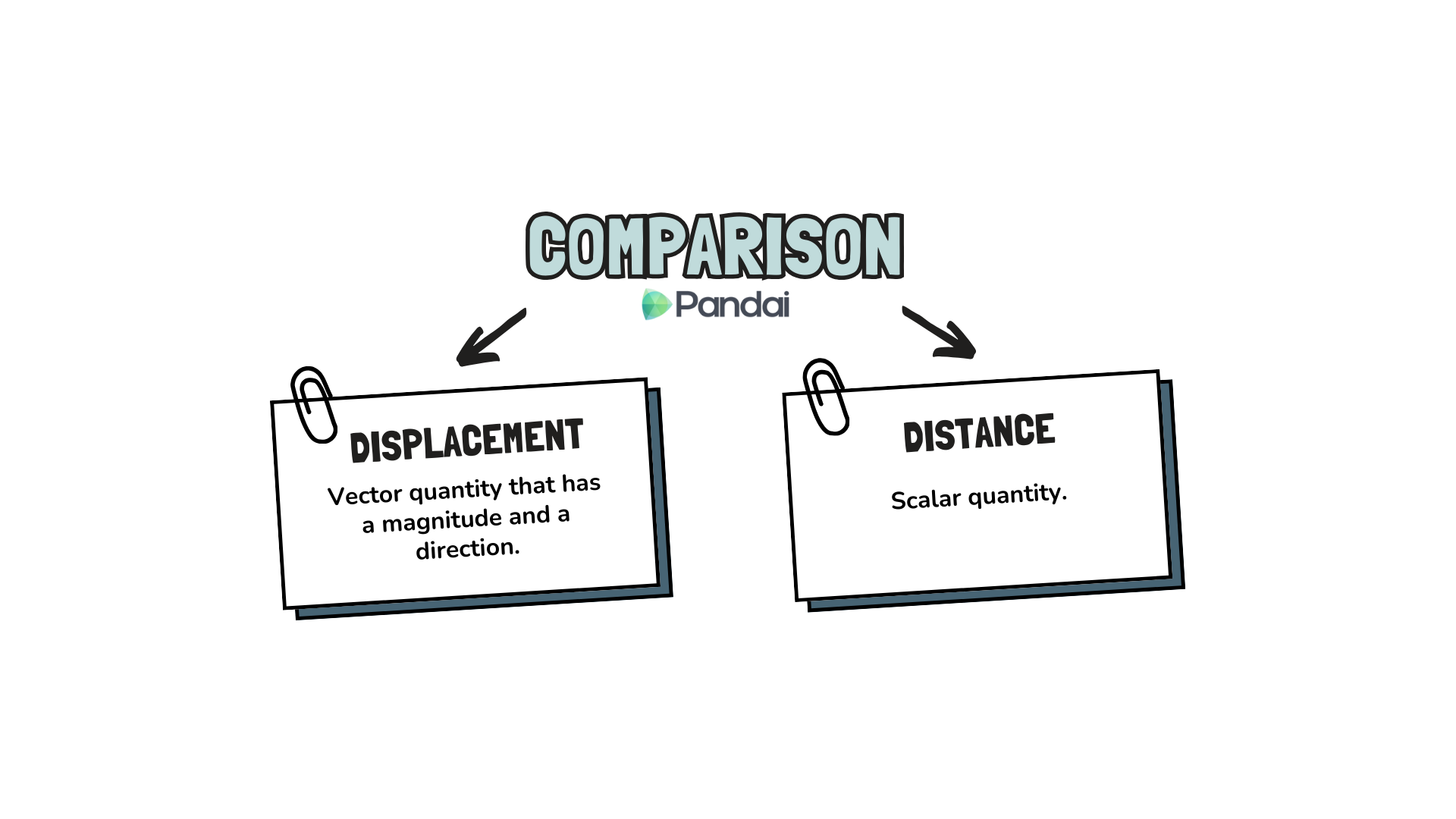
Displacement, \(s\) of a particle from a fixed point is the distance of the particle from the fixed point measured on a certain direction.
|
|
Distance is a scalar quantity that refers to the total path travelled by an object.
|
| Instantaneous Displacement |
The displacement of a particle at a certain time.
|
|
If \(O\) is a fixed point and the movement of a particle to the right is positive, then
- The displacement is negative, \(s\lt0\), meaning the particle is on the left of point \(O\).
- The displacement is zero, \(s=0\), meaning the particle is on the point \(O\).
- The displacement is positive, \(s\gt 0\), meaning the particle is on the right of point \(O\).
|
|
|
|
| Velocity and Speed |
|
A velocity, \(v\) is a vector quantity which defined as the rate of change of displacement with time.
|
|
Speed is a scalar quantity which defined as the rate of change of distance with time.
|
|
The velocity of an object at a certain time.
|
|
If \(O\) is a fixed point and the movement of a particle to the right is positive, then
- The velocity is positive, \(v\gt 0\), meaning that the particle moves to the right.
- The velocity is zero, \(v=0\), meaning that the particle is at rest, that is, the particle is stationary.
- The velocity is negative, \(v\lt 0\), meaning that the particle moves to the left.
|
|
| |
| Acceleration |
|
Acceleration, \(a\) is the rate of change of velocity with time. The acceleration function, \(a\) is a function of time, \(a=f(t)\) and is a vector quantity that has magnitude and direction.
|
|
The rate of change of velocity with time of an object that moves is the same at any time.
|
|
The rate of change of velocity with time of an object that moves is different at any time.
|
| Instantaneous Acceleration |
An acceleration, \(a\) at a certain time, \(t\) and can be obtained by determining the gradient of tangent of velocity-time graph at time, \(t\).
|
|
If the movement of a particle to the right is positive, then
- The acceleration is positive, \(a\gt 0\), meaning the velocity of particle is increasing with time.
- The acceleration is zero, \(a=0\), meaning the velocity of particle is either maximum or minimum.
- The acceleration is negative, \(a\lt 0\), meaning the velocity of particle is decreasing with time.
|
|
| |
| Example |
|
A particle moves along a straight line and passes through a fixed point \(O\).
| (a) |
Its displacement, \(s\) m, of the particle \(t\) seconds after it starts moving is given as |
| |
\(s=4+8t-t^2\). |
| |
Calculate the instantaneous displacement, in m, and determine the position of the particle from point \(O\) when \(t=10\). |
| |
|
| (b) |
Its velocity, \(v\) ms\(^{-1}\), at \(t\) after passing through the point \(O\) is given by |
| |
\(v=3t-12\). |
| |
Calculate the initial velocity in ms\(^{-1}\), of the particle. |
| |
|
| (c) |
At \(t\) seconds after passing through \(O\), its acceleration, \(a\) ms\(^{-2}\), is given by |
| |
\(a=12-4t\). |
| |
Calculate the instantaneous acceleration, in ms\(^{-2}\), of the particle when \(t=7\). |
|
|
(a)
Given \(s=4+8t-t^2\).
When \(t=10\),
\(s=4+8(10)-(10)^2\\ s=4+80-100\\ s=-16.\)
Therefore, the particle is located \(16\) m from the fixed point \(O\) when \(t=10\).
(b)
Given \(v=3t-12\).
At initial velocity, \(t=0\),
\(v=3(0)-12\\ v=-12.\)
Hence, the initial velocity of the particle is \(-12\) ms\(^{-1}\).
(c)
Given \(a=12-4t\).
When \(t=7\),
\(a=12-4(7)\\ a=-16.\)
Therefore, the instantaneous acceleration of the particle when \(t=7\) is \(-16\) ms\(^{-2}\).
|
|
| |