|
Here is Farid's height and mass.
Height: \(1.4\text{ m}\)
Weight: \(36\text{ kg}\)
Does Farid have an ideal body mass?
| BMI \((\text{ kg/m}^2)\) |
You have: |
| \(<18.5\) |
underweight |
| \(18.5-24.9\) |
ideal weight |
| \(25-30\) |
overweight |
| \(30\) or more |
obes |
\(\text{BMI } = \dfrac{\text{Body mass (kg)}}{\text{Height (m)}\times \text{Height(m)}}\\\ \\ \quad\space\space\space=\dfrac{36}{1.4\times 1.4}\\\ \\ \quad\space\space\space=\dfrac{36}{1.96}\\\ \\ \quad\space\space\space=18.37\)
Farid's BMI is \(18.37\text{ kg/m}^2\). Therefore, Farid has ideal body mass. 
The picture below shows the volume of water in two containers, R and S.
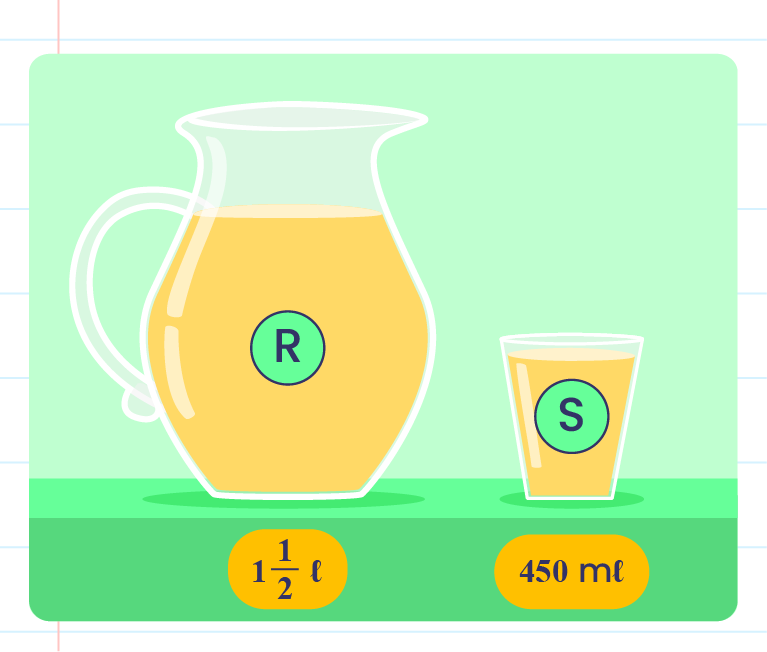
Mrs Jim wants to prepare some syrup. She dissolves 180 g of sugar in container R. How much sugar, in g, should be dissolved in container S so that both the containers have the same concentration of syrup?
Container R: \(1\dfrac{1}{2}\,m\ell=1500\,\ell\)
\(1\ 500\ ml\) → \(180\ g\)
\(1\ ml\) → \(\dfrac{180\ g}{1500\ ml}\)
\(450\ ml\) → \(\dfrac{180\ g}{1500\ ml}\times450\ ml=54\ g \)
|