| |
| 4.1 |
Scale Drawings |
| |
| |
Definition |
|
| |
|
|
| |
The drawing of an object with all measurements in the drawing proportional to the measurements of the object.
|
|
|
| |
| Interpret the scale of a scale drawing: |
| |
| \(\begin{aligned}&\space\text{Scale}\\\\&=\dfrac{\text{Measurement of scale drawing}}{\text{Measurement of object}}\end{aligned}\) |
| |
|
The ratio is,
- Measurement of scale drawing : Measurement of object
|
| |
|
Scale drawings in the form of ratio is,
\(1:n\), where \(n\) is the positive integer or fraction.
|
| |
|
\(1:n\) means one unit on the scale drawing will represent \(n\) units on the object.
|
| |
|
|
| |
|
|
| |
|
|
| |
| |
Example |
|
| |
|
|
| |
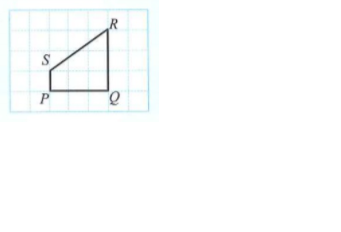
The diagram below shows object \(PQRS\) and scale drawing \(P'Q'R'S'\) drawn on a grid of equal squares.
|
|
| |
|
|
| |
State the scale used in the form of \(1:n\).
|
|
| |
|
|
| |
\(\text{Scale}=\dfrac{P'Q'}{PQ}=\dfrac{2}{4}=\dfrac{1}{2}\) or,
\(\text{Scale}= \dfrac{P'S'}{PS}=\dfrac{3}{6}=\dfrac{1}{2}\).
|
|
| |
|
|
| |
Thus, \(\text{scale}=1:2\). |
|
|
| |
| |
Example |
|
| |
|
|
| |
A map is drawn to a scale of \(1 : 400 \space000\).
Calculate the actual length, in \(\text{km}\), of a river that is \(4\text { cm}\) long on the map.
|
|
| |
|
|
| |
\(\begin{aligned} \dfrac {1 \text{ cm}}{400 \space 000 \text{ cm}}& = \dfrac{4 \text{ cm}}{ \text{Actual distance}} \end{aligned} \)
\(\begin{aligned} \\&\space\text{Actual distance}\\\\&=\dfrac{4 \times 400 \space000 \text{ cm}}{1\text{ cm}} \\\\&=1 \space 600 \space 000 \text{ cm} \\\\&=16 \text{ km}. \end{aligned}\)
Thus, the actual length of the river is \(16\text{ km}\).
|
|
|
| |
| Drawing the scale drawing of an object: |
| |
|
Three ways to draw the scale drawing of an object are,
- Use grid paper of the same size for different scales.
- Use grid paper of different sizes.
- Draw on a blank paper according to the given scale.
|
| |
| |
Example |
|
| |
|
|
| |
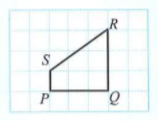
Draw the scale drawing of shape \(PQRS\) on a grid of equal squares using a scale of \(1 :\dfrac{1 }{2}\).
|
|
| |
|
|
| |
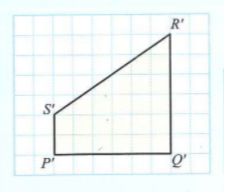
The scale given is \(1 :\dfrac{1 }{2}\).
Therefore, every side of the scale drawing is two times longer than the length of the sides of object \(PQRS\).
|
|
|
| |
| Problem solving: |
| |
| |
Example |
|
| |
|
|
| |
The distance on a map between Kuantan and Gombak is \(4 \text { cm}\).
a) If the scale used to draw map is \(1\text { cm}: 50 \text{ km}\), calculate the actual distance, in \(\text{km}\), between Kuantan and Gombak.
b) Mr. Danish wants to visit Kuantan.
If he plans to drive to Kuantan at a speed of \(100\text{ km h}^{-1}\), calculate the time taken to drive from Gombak to Kuantan in hours.
|
|
| |
|
|
| |
a) Solution:
\(\begin{aligned} \text{Scale}&=\dfrac{\text{Drawing distance}}{\text{Actual distance}} \\\\\dfrac{1}{50 \text{ km}}&=\dfrac{4\text{ cm}}{\text{Actual distance}} \\\\\text{Actual distance}&= \dfrac{4\text { cm}(50 \text{ km})}{1\text{ cm}} \\\\&= 200 \text{ km}. \end{aligned}\)
|
|
| |
|
|
| |
b) Solution:
\(\begin{aligned} \text{Time}&=\dfrac{\text{Distance}}{\text{Speed}}\\\\&= \dfrac {200 \text { km }} {100 \text{ km h}^{-1}} \\\\&= 2{\text{ hours}}. \end{aligned}\)
|
|
|
| |