| |
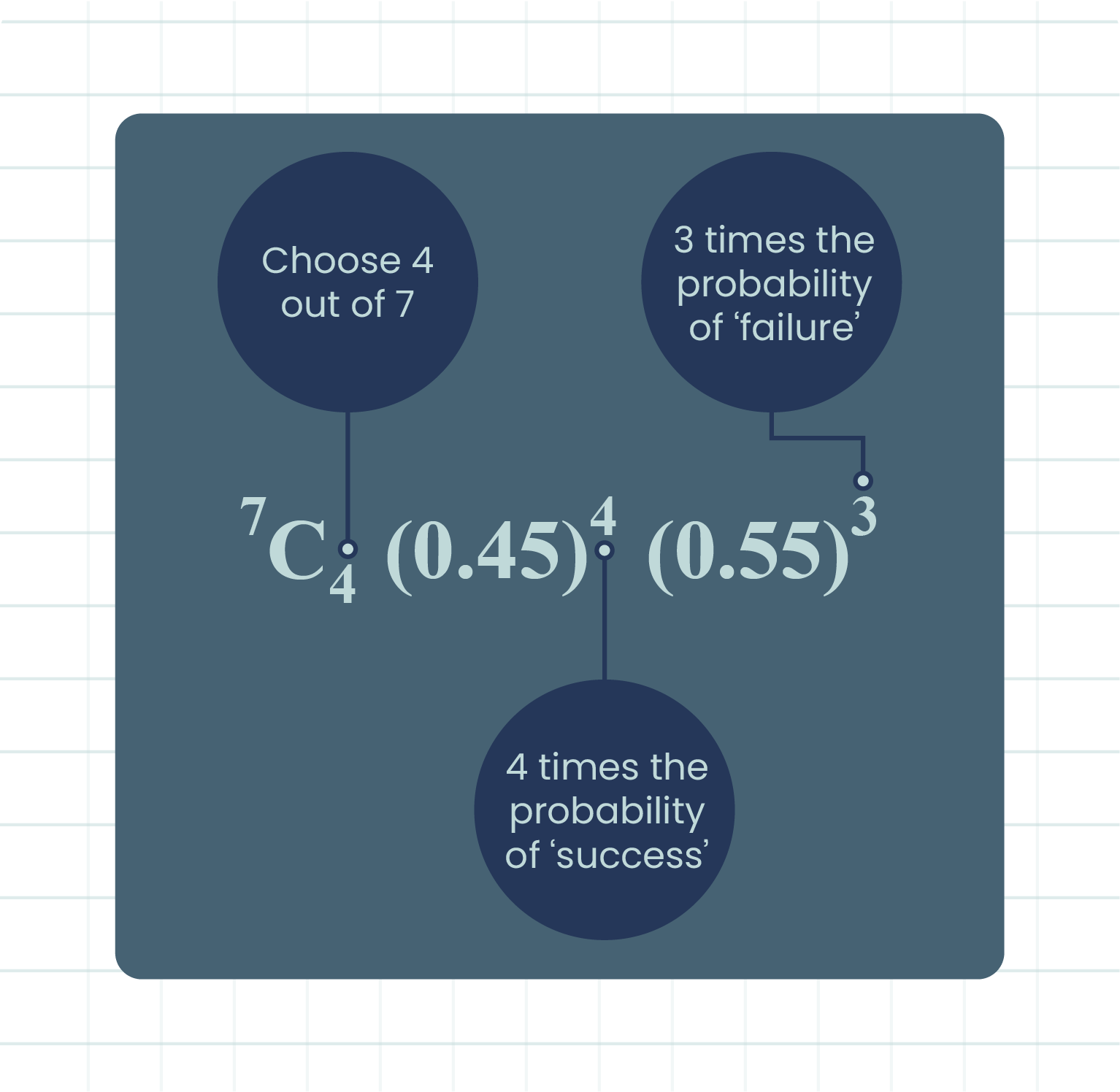 |
| |
| |
|
|
| |
- When \(p=0.5\), the graph is symmetrical.
-
When \(p\text{ < }0.5\), the graph is skewed to the left and is not symmetrical.
-
When \(p\text{ > }0.5\), the graph is skewed to the right and is not symmetrical.
|
|
| |
|
|
|
|
| |
| Example |
| |
|
|
| |
Emma did a survey on the percentage of pupils in her school who use school buses to come to school.
It is found that \(45\%\) of pupils from her school use school buses.
A sample of \(4\) pupils is randomly selected from the school.
|
|
| |
|
|
| |
| (a) |
Construct a binomial probability distribution table for the number of pupils who use school bus.
|
| |
|
| (b) |
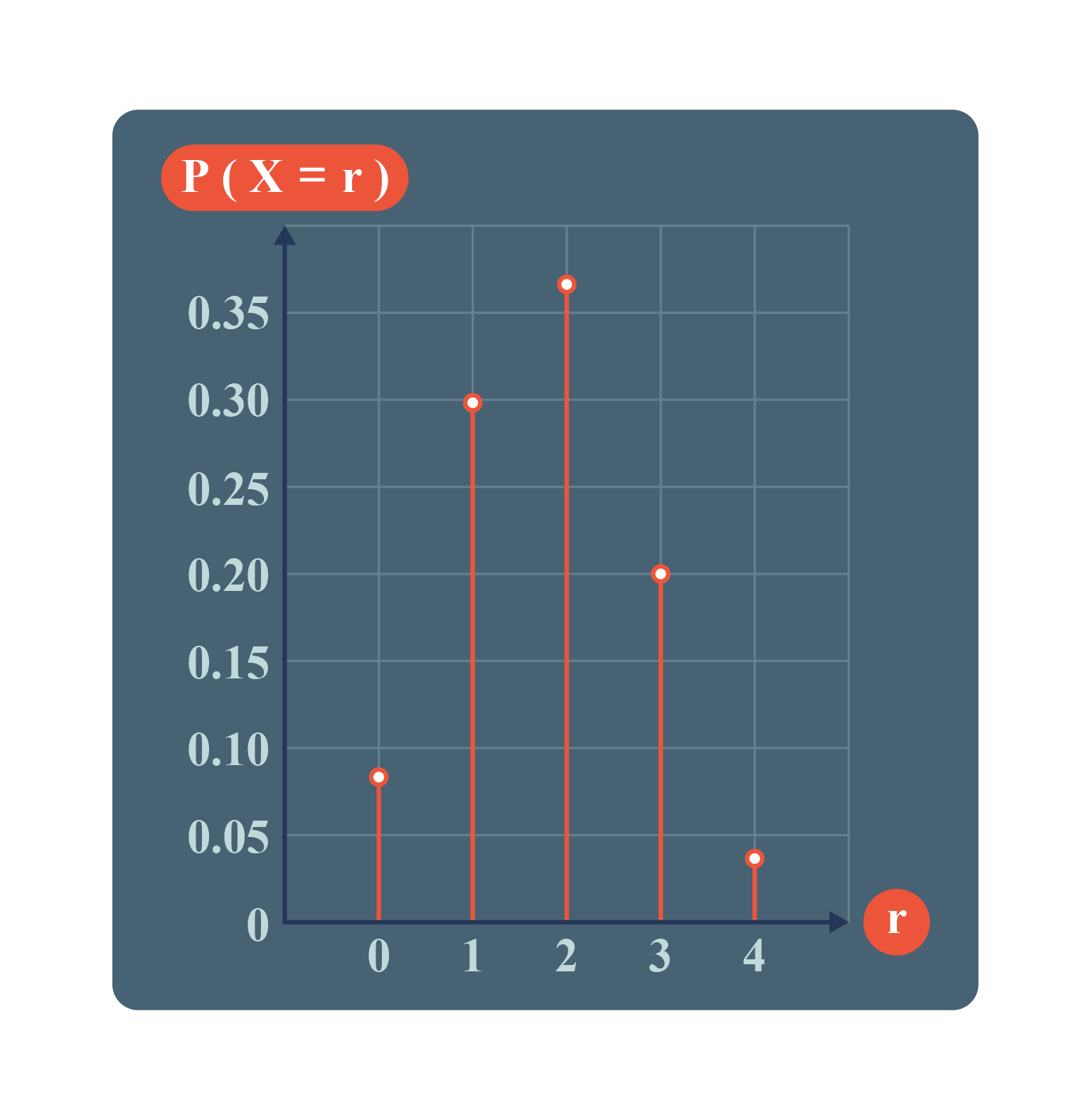
Draw a graph for this distribution.
|
| |
|
| (c) |
From the table or graph, find the probability that
|
| |
| |
|
| (i) |
more than \(3\) pupils come to school by school buses,
|
| (ii) |
less than \(2\) pupils use school buses.
|
| |
|
|
| |
|
| Solution: |
| |
|
| (a) |
Let \(X\) epresent the number of pupils who use school buses.
Then, \( X = \lbrace 0, 1, 2, 3, 4\rbrace\).
Given \(n=4, \ p=0.45 \text{ and }q=0.55\).
|
| |
|
| |
| \(X=r\) |
\(P(X=r)\) |
| \(0\) |
\(^{4}C_{0}(0.45)^0(0.55)^4 = 0.0915\) |
| \(1\) |
\(^{4}C_{1}(0.45)^1(0.55)^3 = 0.2995\) |
| \(2\) |
\(^{4}C_{2}(0.45)^2(0.55)^2 = 0.3675\) |
| \(3\) |
\(^{4}C_{3}(0.45)^3(0.55)^1 = 0.2005\) |
| \(4\) |
\(^{4}C_{4}(0.45)^4(0.55)^0 = 0.0410\) |
|
| |
|
| (b) |
 |
| |
|
| (c) |
| (i) |
\(\begin{aligned} P(X\text{ > }3) &= P(X=4)\\ &=0.0410 \end{aligned}\) |
| |
|
| (ii) |
\(\begin{aligned} P(X\text{ < }2) &= P(X=0) + P(X=1)\\ &=0.0915+0.2995\\ &=0.3910 \end{aligned}\) |
| |
|
|
|
|
|
|
| |
-
If a discrete random variable \(X\) has a binomial distribution, that is, \(X \sim\text{B}(n,p)\), then the expected value or mean, \(\mu\) can be defined as:
|
| |
| Expected Value or Mean, \(\mu\) |
| |
|
|
| |
The sum of the product of the value of \(X\) with its respective probability divided by the total probability of the distribution.
|
|
| |
|
|
|
|
| |
| |
|
|
| |
\(\mu = \dfrac{\sum_{i=0}^{n}\ r \ P(X = r)}{\sum_{i=0}^{n}\ P(X = r)}\) |
|
| |
|
|
|
|
| |
- Since \(\sum_{i=0}^{n}\ P(X = r) = 1 \), then the mean, \(\mu\):
- Standard deviation, \(\sigma\) is a measure of deviation of a set of data from its mean value:
|
| |
| Example |
| |
|
|
| |
A study shows that \(95\%\) of Malaysians aged \(20\) and above have a driving license.
If \(160\) people are randomly selected from this age group, estimate the number of Malaysians aged \(20\) and above who have a driving license.
Then, find the variance and the standard deviation of the distribution.
|
|
| |
|
|
| |
|
|
| |
Solution: |
|
| |
|
|
| |
Given \(p = 0.95, \ q = 0.05 \text{ and } n = 160.\)
\(\begin{aligned} \text{Mean, } \mu&=np\\ &=160\times 0.95\\ &= 152 \end{aligned}\)
\(\begin{aligned} \text{Variance, } \sigma^2 &=npq\\ &=160\times 0.95 \times 0.05\\ &= 7.60 \end{aligned}\)
\(\begin{aligned} \text{Standard deviation, } \sigma&=\sqrt{npq}\\ &=\sqrt{7.60}\\ &= 2.76 \end{aligned}\)
|
|
| |
|
|
|
|
| |