|
Given an arrow diagram of a function:
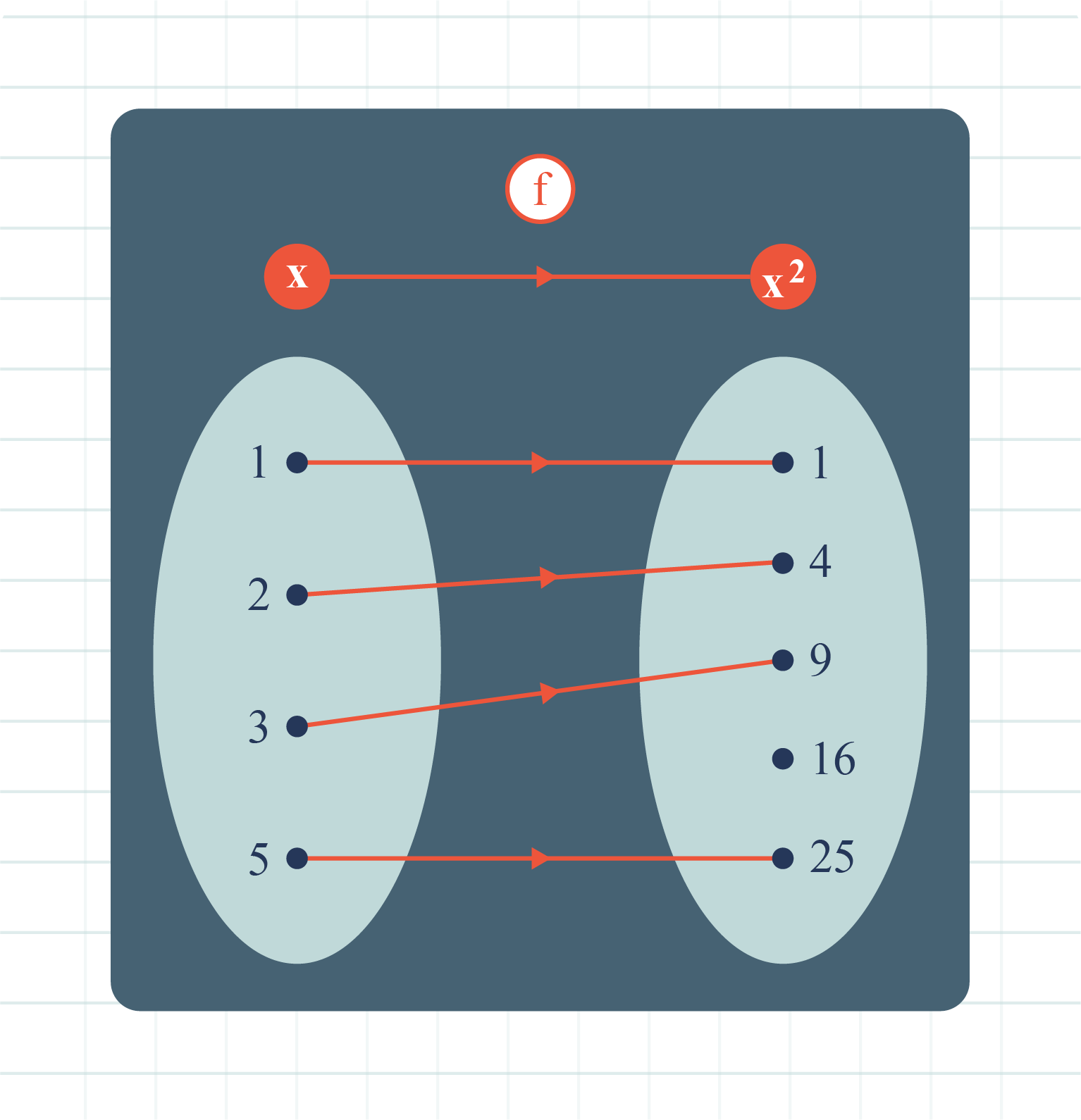
Find the domain, codomain and range for the function, hence
state the object of \(4\) and image of \(3\)
|
|
From the diagram above,
Domain \(=\lbrace1,\,2, \, 3,\,5 \rbrace\),
Codomain \(=\lbrace1,\,4, \, 9,\,16,\,25 \rbrace\),
Range \(=\lbrace1,\,4, \, 9,\,25 \rbrace\).
Next,
Object of \(4\) is \(2\) and image of \(3\) is \(9\).
|