| |
| We will learn to solve basic operations involving fractions. |
| |
- An improper fraction is a fraction with the numerator equal to or greater than the denominator.
|
| |
|
As example,
\(\dfrac{24}{5}\) is an improper fraction because the value of the numerator (\(\color{red}{24}\)) is greater than the value of the denominator (\(\color{red}{5}\)).
|
| |
- A mixed number consists of a whole number and a proper fraction.
|
| |
|
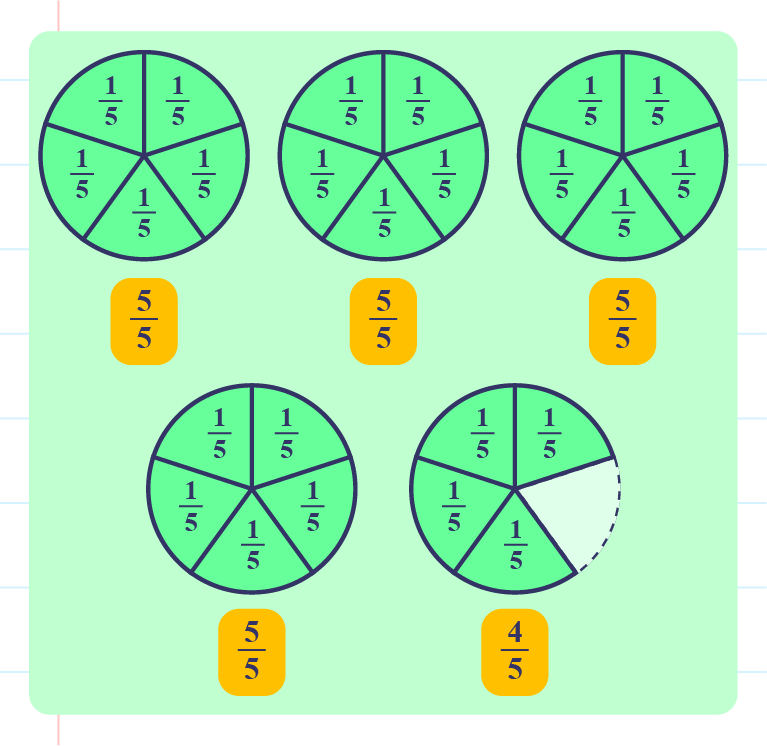
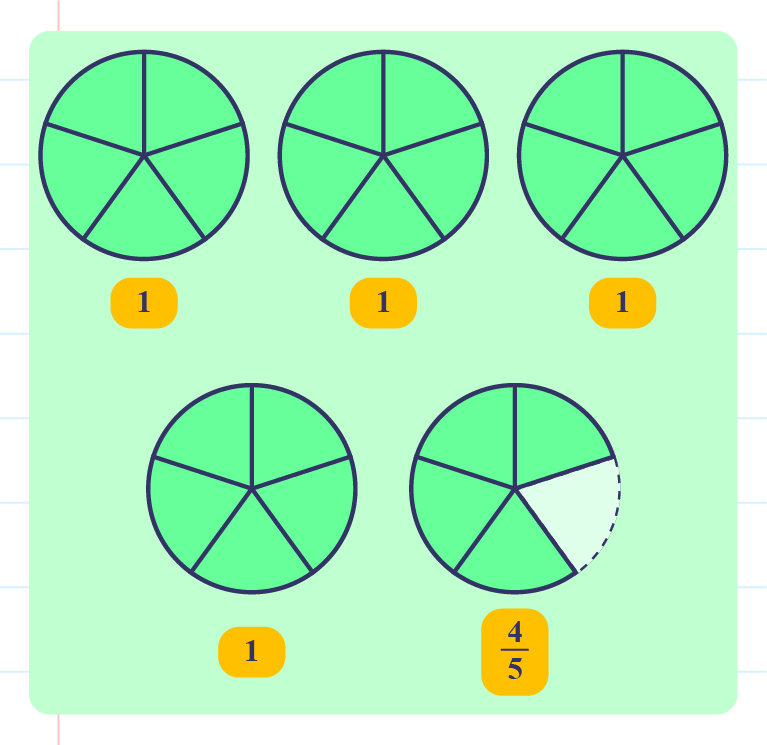
As example,\(\dfrac{24}{5}\) can be converted to mixed numbers as follows:
|
| |
 |
 |
 |
| |
|
Based on the above picture, \(\dfrac{24}{5}=\color{magenta}{4\dfrac{4}{5}}\).
|
| |
|
Or, the simple steps to convert improper fractions to mixed numbers are as follows:
\(\begin{aligned}\space \space 4 \\5\space\overline{)2\space4} \\\underline{-\space2\space0}\\4 \end{aligned}\)\(=\color{magenta}{4\dfrac{4}{5}}\)
|
| |
|
The simple steps to convert mixed numbers to improper fractions are as follows:
\(\begin {aligned} \color{black}{4\dfrac{4}{5}} &= \dfrac {4 \times 5 +4}{5} \\ &= \color{magenta}{\dfrac {24}{5}} \end {aligned}\)
|
| |
| |
- To add fractions with the same denominators, add the numerators without changing the denominators.
|
| |
|
As example,
\(\begin{aligned} \dfrac{1}{5}+\dfrac{2}{5}&=\dfrac{1+2}{5} \\&=\color{red}{\dfrac{3}{5}} \end{aligned}\)
|
| |
- To add fractions with different denominators, find the common multiple value of the denominator.
|
| |
|
As example,
\(\begin{aligned} \dfrac{1}{6}+\dfrac{3}{4}&=\dfrac{1{\color{green}{\times2}}}{6{\color{green}{\times2}}}+\dfrac{3{\color{green}{\times3}}}{4{\color{green}{\times3}} }\\&=\dfrac{2}{12}+\dfrac{9}{12} \\&={\color{magenta}{\dfrac{11}{12}}} \end{aligned}\)
|
| |
| |
- To subtract fractions with the same denominator, the subtraction operation is performed as usual.
|
| |
| The denominator is retained. |
| |
|
As example,
\(1-\dfrac{2}{5}=\underline{\hspace{1cm}}\)
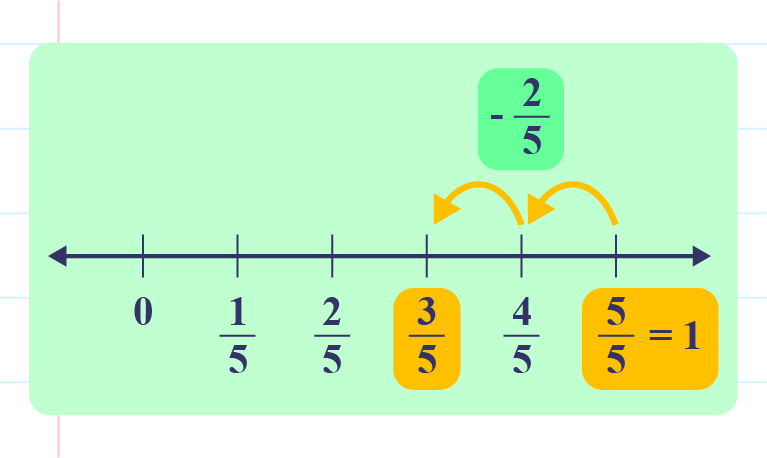
Thus, \(1-\dfrac{2}{5}=\color{magenta}{\dfrac{3}{5}}\).
|
| |
|
To subtract the fractions with different denominators, change to equivalent fractions with the same denominators before subtracting the numerators.
|
| |
| Retain the denominator. |
| |
|
As example,
\(\begin{aligned} \dfrac{3}{5}-\dfrac{1}{2}&=\dfrac{3\color{green}{\times2}}{5\color{green}{\times2}}-\dfrac{1\color{green}{\times5}}{2\color{green}{\times5}} \\&=\dfrac{6}{10}-\dfrac{5}{10} \\&={\color{magenta}{\dfrac{1}{10}}} \end{aligned}\)
|
| |
| |
- For mixed operations involving the addition and subtraction of fractions, the calculation is done from the left to the right.
|
| |
|
As example,
\(\begin{aligned} \dfrac{1}{7}+\dfrac{5}{7}-\dfrac{2}{7}&=\dfrac{1+5-2}{7} \\&={\color{red}{\dfrac{4}{7}}} \end{aligned}\)
|
| |
|
|
| |
|
As example,
find the value of \(\dfrac{5}{7}\) from \(56\).
|
| |
| \(\begin{aligned} \dfrac{5}{7}\text{ from }56&=\dfrac{5}{7}\times56 \\&=\dfrac{5\times56}{7} \\&=\dfrac{280}{7} \\&={\color{red}{40}} \end{aligned}\) |
| |