| Relationship Between a Network and a Graph |
|
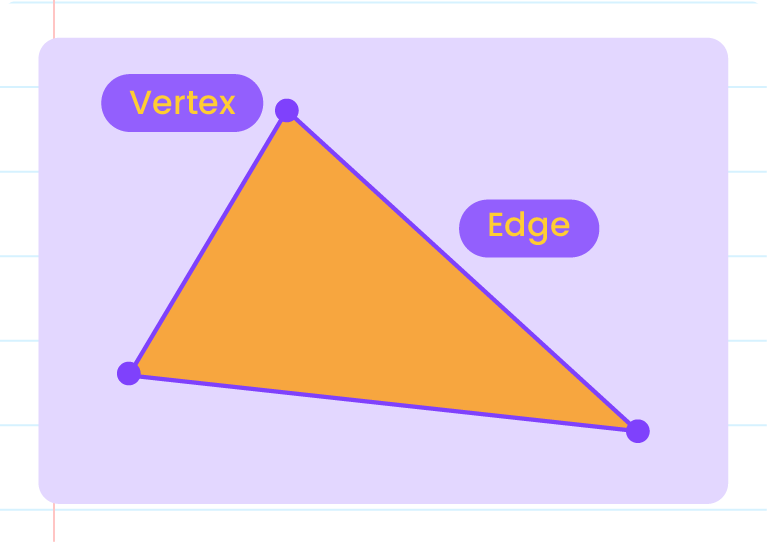
- A graph represents discrete data and shows the relationships between objects in a simple, visual way.
- A graph is a series of dots connected or not connected by lines.
- Each dot is known as a vertex, and the line joining two vertices is known as an edge.
- A graph typically represents a network.
- A network is a part of a graph where the vertices and edges have specific characteristics.
- The structure of network data has a many-to-many relationship.
|
| The Sum of Degrees of a Graph |
\(\sum d(v)=2E;v \isin V\)
| \(G\) |
Graph |
| \(d\) |
Degree |
| \(v\) |
Vertex or Dot |
| \(V\) |
Set of Dots or Vertices |
| \(e\) |
Edge or line or arc |
| \(E\) |
Set of Edges or Lines Linking Each Pair of Vertices |
| \(\sum\) |
Sum |
|
| Simple Graph |
- A simple graph has no loops and no multiple edges.
- The sum of degrees of the graph is twice the number of edges.
|
|
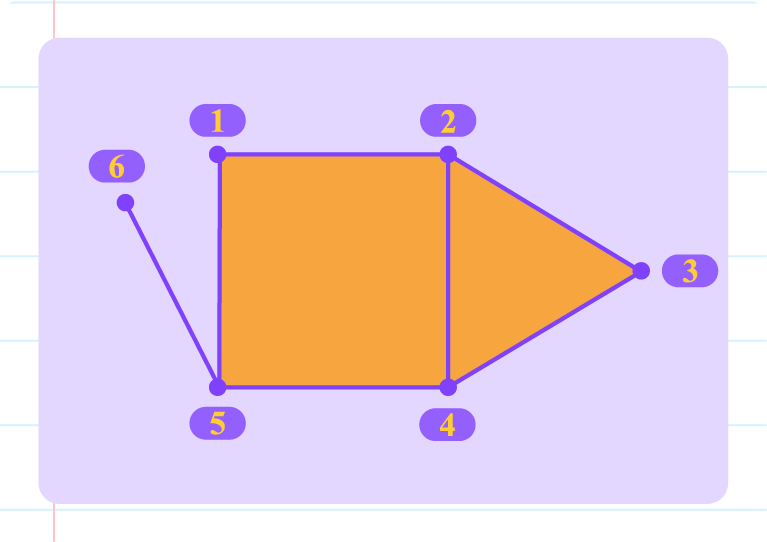
Based on the simple graph given, determine \(V\text{ and }n(V)\), \(E\text{ and }n(E)\) and sum of degrees.
| \(V\text{ and }n(V)\) |
\(\text{Set of vertices}=V=\{1,2,3,4,5,6\}\\\text{Number of vertices}=n(V)=6\color{red}\text{}\) |
| \(E\text{ and }n(E)\) |
\(\text{Set of vertex pairs}=E=\{(1,2),(1,5),(2,3),(2,4),(3,4),(4,5),(5,6)\}\\\text{Number of edges}=n(E)=7\) |
| Sum of Degrees |
\(\sum d(v)=2(E)\\\qquad\quad\;=2(7)\\\qquad\quad\;=14\)
|
|
| Multiple Edges and Loops of a Graph |
| Multiple Edges |
Loops |
- Involve \(2\) vertices.
- The vertices are connected by more than \(1\) edge.
- The sum of degrees is twice the number of edges.
|
- Involve \(1\) vertex.
- The edge in the form of an arc that starts and ends at the same vertex.
- Each loops adds \(2\) to the degree.
|
|
|
The degree of a vertex with a loop in an undirected graph is \(2\), one in clockwise direction and the other in anticlockwise direction. |
|
The diagram below shows a graph with a loop and multiple edges. State \(V\text{ and }n(V)\), \(E\text{ and }n(E)\) and sum of degrees.
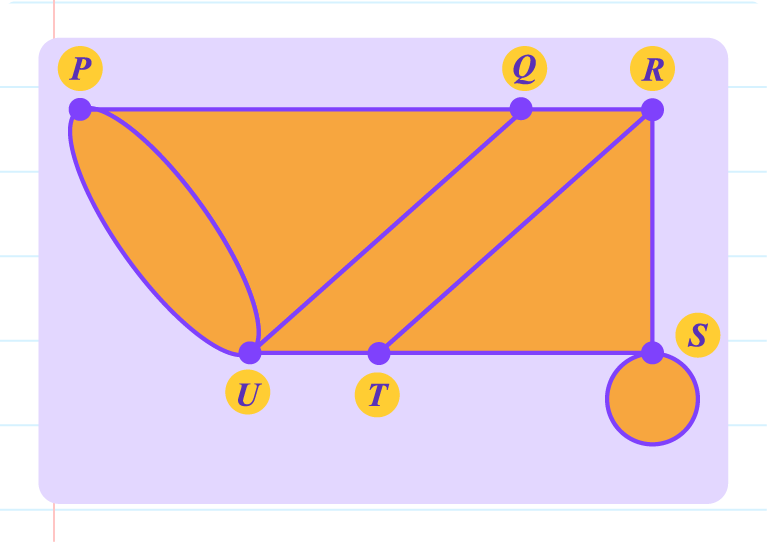
| \(V\text{ and }n(V)\) |
\(V=\{P,Q,R,S,T,U\} \\n(V)=6\color{red}\text{}\) |
| \(E\text{ and }n(E)\) |
\(E=\{(P,Q),(P,U),(P,U),(Q,R),(Q,U),(R,S),(R,T),(S,S),(S,T),(T,U)\} \\n(E)=10\color{red}\text{}\) |
| Sum of Degrees |
\(\text{Degree of vertex }P=3\\\text{Degree of vertex }Q=3\\\text{Degree of vertex }R=3\\\text{Degree of vertex }S=4\\\text{Degree of vertex }T=3\\\text{Degree of vertex }U=4\)
The sum of degrees is \(20\).
|
|
| Difference Between a Directed Graph and an Undirected Graph |
|
|
| Differences Between Weighted Graphs and Unweighted Graphs |
|
| Weighted Graph |
Unweighted Graph |
- Type of graph:
- directed graph
- undirected graph
- Edge:
- associated with a value or a weight
- The edge represents:
- distance between two cities
- travelling time
- the current in an electrical circuit
- cost
|
- Type of graph:
- directed graph
- undirected graph
- Edge:
- not associated with a value or a weight
- The edge relates informaton like:
- job hierarchy in an organisation chart
- flow map
- tree map
- bubble map
|
|
|
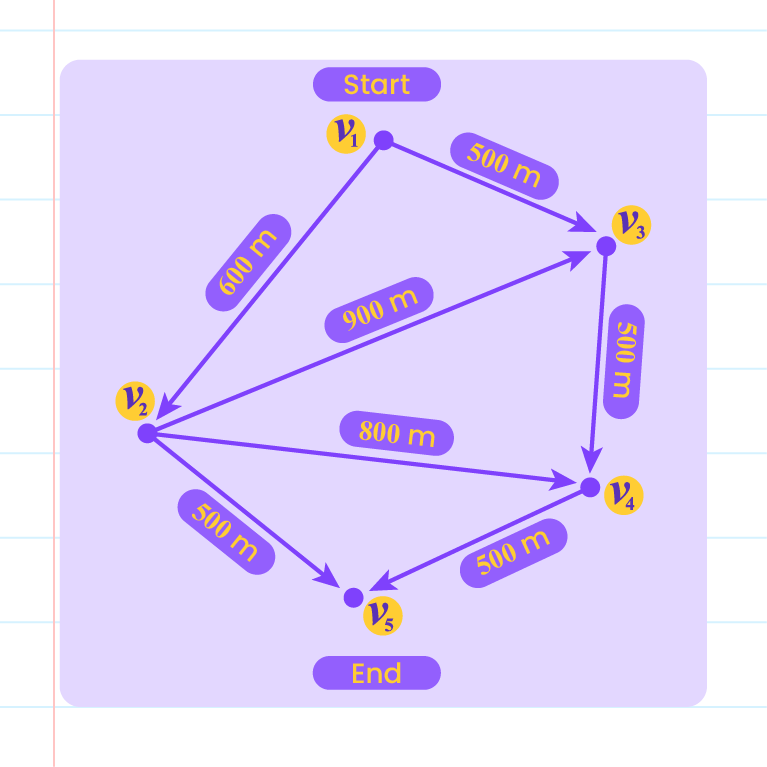
The diagram shows one-way paths that Aiman can choose for his running practice. Vertex \(v_1\) is the starting position and vertex \(v_5\) is the ending position before he goes home.
Determine
- the shortest distance from \(v_1\) to \(v_5\).
- the longest distance from \(v_1\) to \(v_5\).
- the vertices that must be passed through if the distance of the one-way run is between \(1.4\text{ km}\) and \(2.1\text{ km}\).
| |
Solution |
| Shortest distance from \(v_1\) to \(v_5\) |
\(\quad v_1\rightarrow v_2 \rightarrow v_5\\=(600+500)\text{ m}\\=1\,100\text{ m}\\=1.1\text{ km}\) |
| Longest distance from \(v_1\) to \(v_5\) |
\(\quad v_1\rightarrow v_2 \rightarrow v_3\rightarrow v_4 \rightarrow v_5\\=(600+900+500+500)\text{ m}\\=2\,500\text{ m}\\=2.5\text{ km}\) |
The vertices that must be passed through if the distance of the
one-way run is between  \(1.4\text{ km}\) and \(1.4\text{ km}\) and  \(2.1\text{ km}\) \(2.1\text{ km}\) |
\(v_1,v_3,v_4,v_5 \text{ and }v_1,v_2,v_4,v_5\) |
|
| Subgraph |
| A subgraph is part of a graph or the whole graph redrawn without changing the original positions of the vertices and edges. |
|
Determine whether below are the subgraphs of graph \(G\).
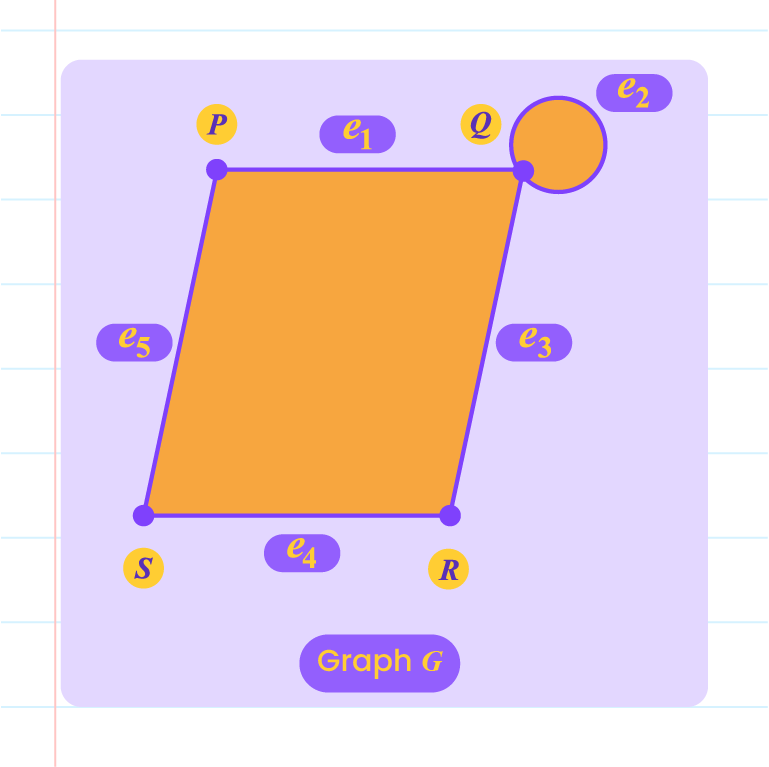
| |
Solution |
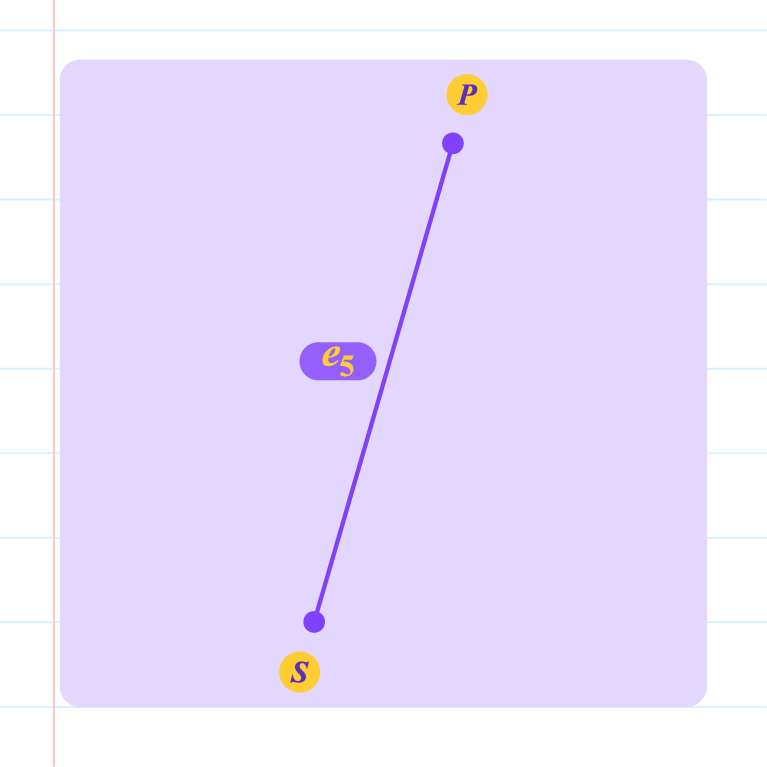 |
Yes, because the vertex pair of edge \(e_5\) is the same.
\(\{e_5\}\subset\{e_1,e_2,e_3,e_4,e_5\}\) and \(\{P,S\}\subset\{P,Q,R,S\}\)
|
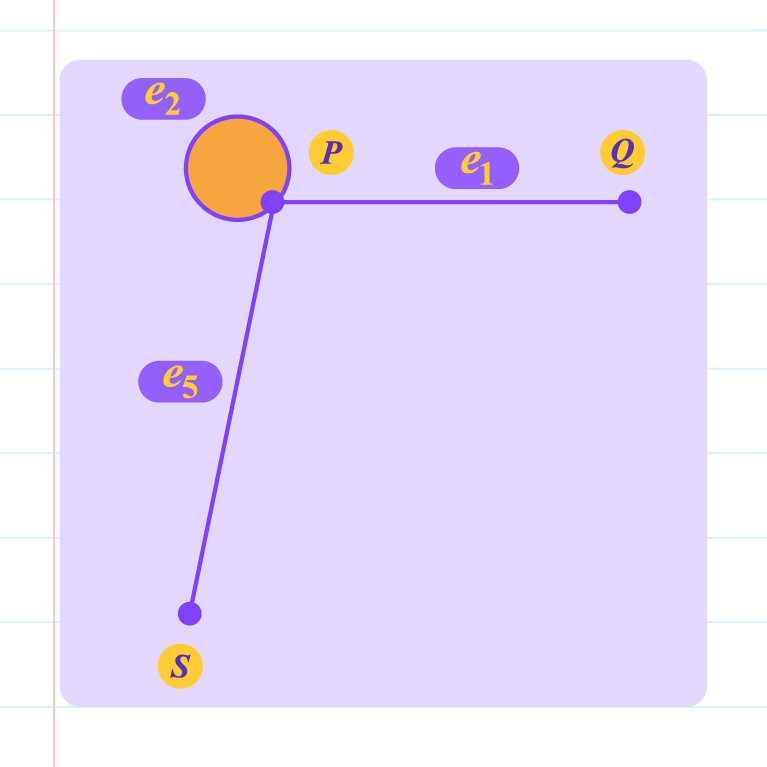 |
No, because the position of loop \(e_2\) is not on vertex \(Q\). |
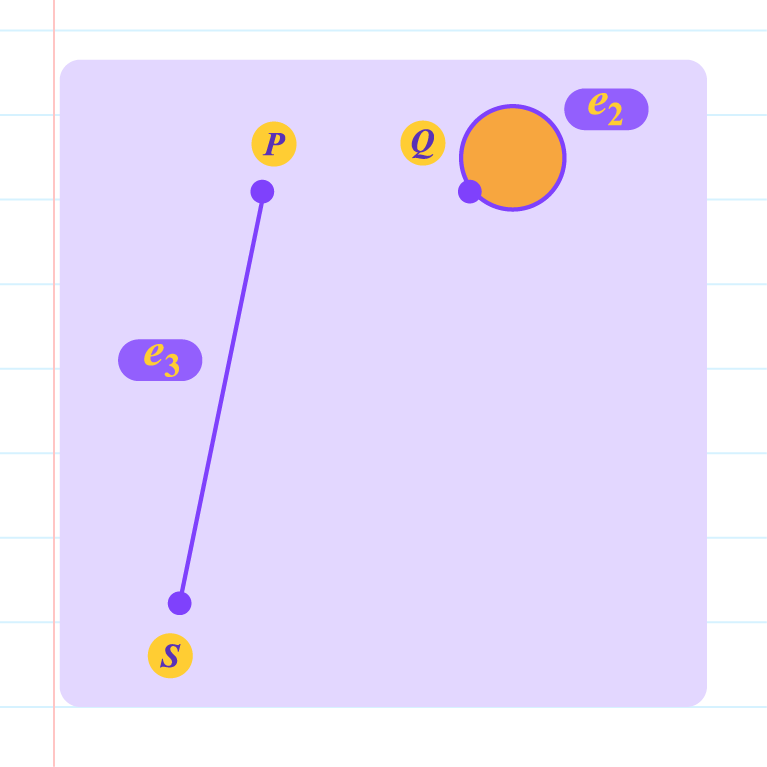 |
No, because the edge connecting vertex \(P\) and vertex \(S\) is not \(e_3\). |
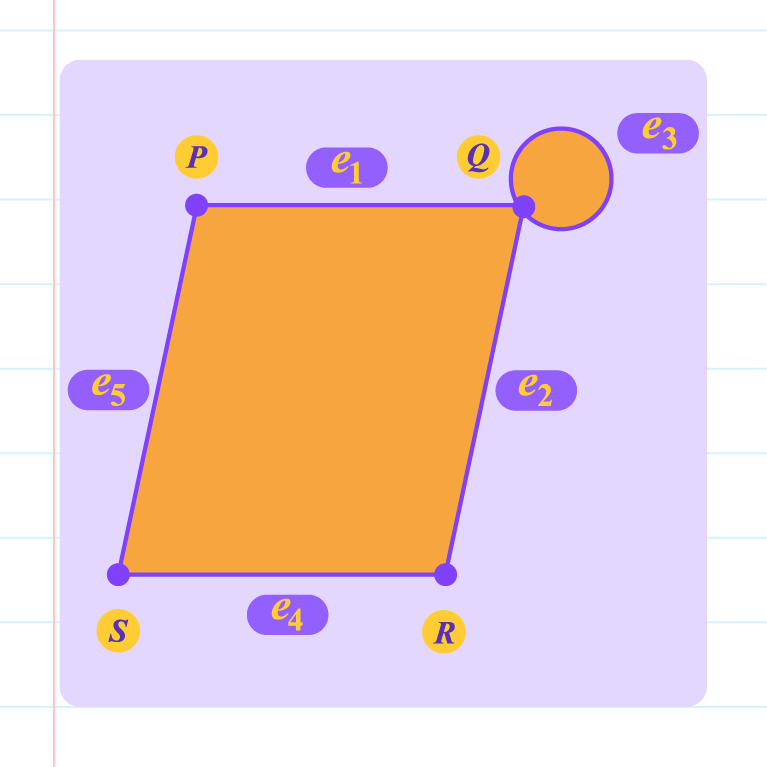 |
No, because the loop and and the edge connecting vertex \(Q\) and vertex \(R\) are wrong. |
|
| Tree |
|
A tree of a graph is a subgraph of the graph with the following properties:
- A simple graph without loops and multiple edges.
- All the vertices are connected and each pair of vertices is connected by only one edge.
- \(\text{Number of edges}=\text{Number of vertices}-1\\\text{Number of vertices}=n\\\text{Number of edges}=n-1\)
|
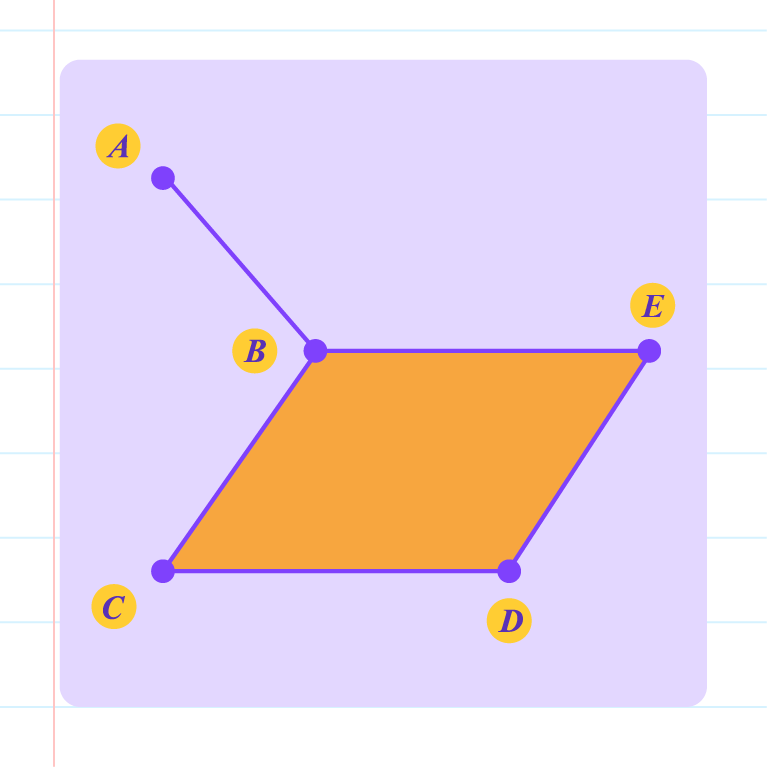
 |
Tree, because
- all the vertices are connected.
- every pair of vertices is connected by an edge only.
- there are no loops or multiple edged.
- \(5\) vertices, \(4\) edges.
|
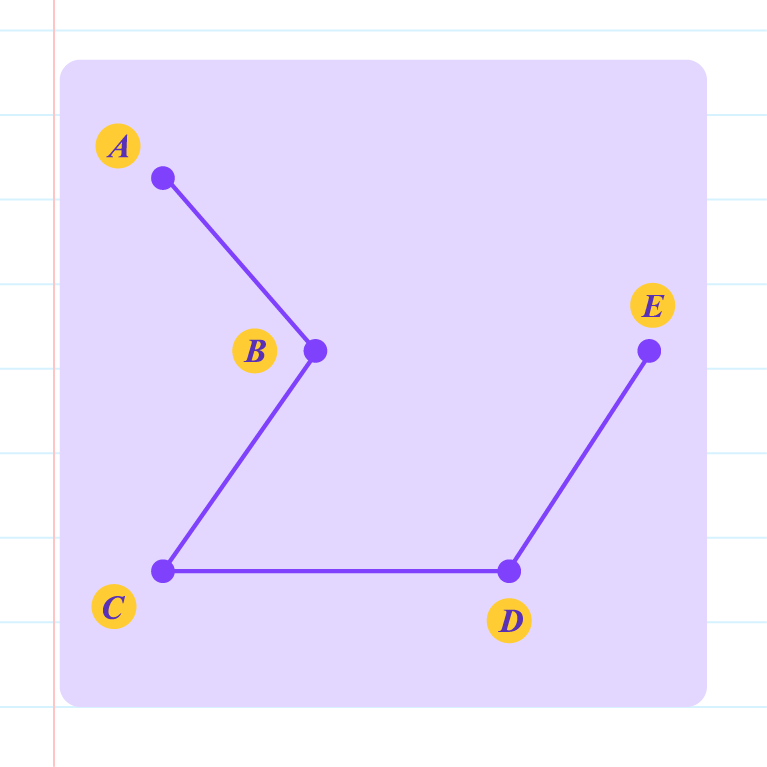
 |
Not a tree, because
- vertex \(B\) and vertex \(E\) can be connected in two ways
- \(B \rightarrow E\)
- \(B \rightarrow C \rightarrow D \rightarrow E\)
- \(5\) vertices, \(5\) edges.
|
|
|
The following diagram shows an undirected weighted graph. Draw a tree with a minimum total weight.
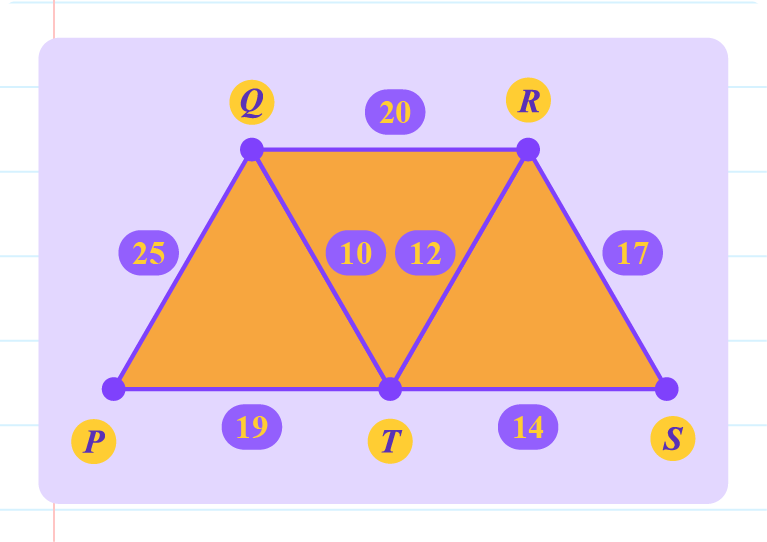
Solution:
| Step \(1\) |
Step \(2\) |
- \(5\) vertices, \(7\) edges.
- \(3\) edges to be removed.
- Remove edges with the greatest weights \((PQ, QR, PT)\).
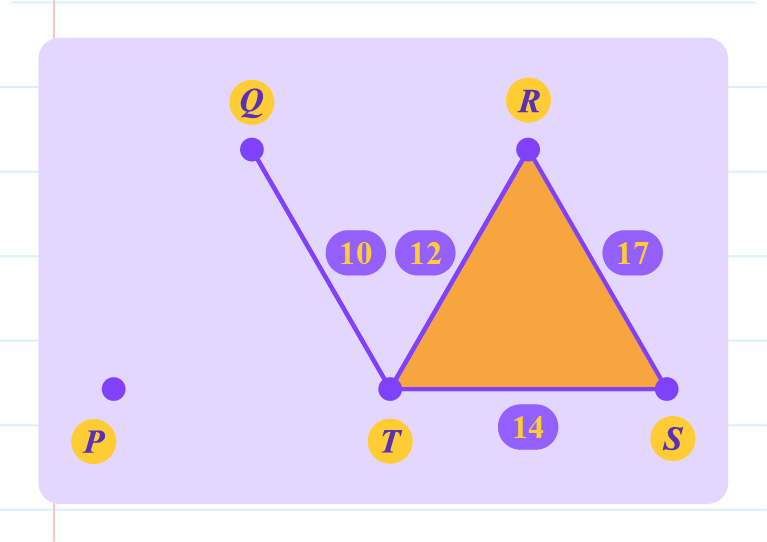
The graph above is not a tree because
- vertex \(P\) is not connected to the other vertices.
- \(3\) edges, \(RS,ST\) and \(RT\), connect \(3\) vertices only.
|
- Between the weights \(19\) and \(25\), keep weight \(19\) because its weight is smaller.
- Between the weights \(12\), \(14\) and \(17\), remove weight \(17\).
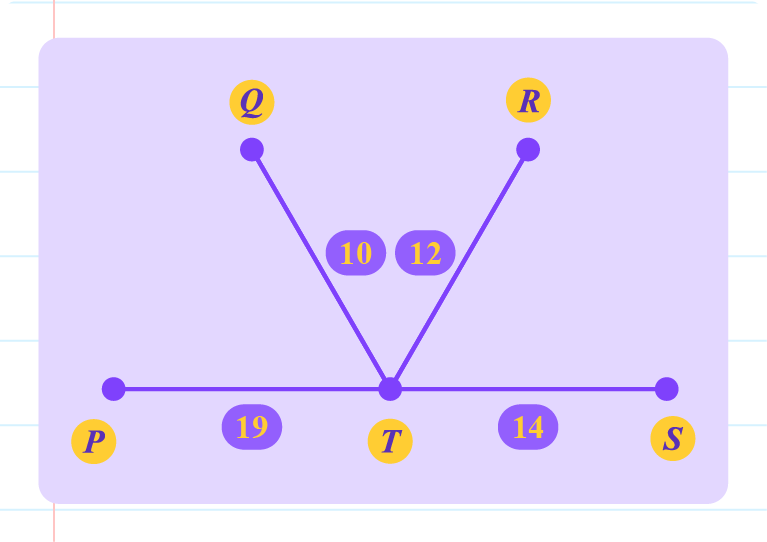
The graph above is a tree.
Minimum total weight of the tree
\(=10+12+14+19\\=55\)
|
|
|