| Union of Sets |
- The union of sets \(P\) and \(Q\) is written using the symbol \(\cup\).
- \(P \cup Q\) represents all the elements in set \(P\) or set \(Q\) or in both sets \(P\) and \(Q\).
|
| The Union of Two or More Sets Using The Venn Diagram |
 |
|
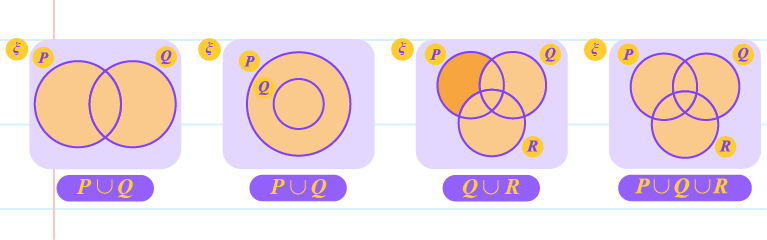It is given that set \(P=\{\text{factors of 24}\}\), set \(Q=\{\text{multiples of 3 which are less than 20}\}\) and set \(R=\{\text{multiples of 4 which are less than 20}\}\).
List all the elements of \(P \cup Q\), \(P \cup R\), \(Q \cup R\) and \(P\cup Q \cup R\).
| \(P \cup Q\) |
\(P=\{1,2,3,4,6,8,12,24\}\)
\(Q=\{3,6,9,12,15,18\}\)
\(P\,\cup Q=\{1,2,3,4,6,8,9,12,15,18,24\}\) |
| \(P \cup R\) |
\(P=\{1,2,3,4,6,8,12,24\}\)
\(R=\{4,8,12,16\}\)
\(P\,\cup R=\{1,2,3,4,6,8,12,16,24\}\) |
| \(Q \cup R\) |
\(Q=\{3,6,9,12,15,18\}\)
\(R=\{4,8,12,16\}\)
\(Q\,\cup R=\{3,4,6,8,9,12,15,16,18\}\) |
| \(P\cup Q \cup R\) |
\(P=\{1,2,3,4,6,8,12,24\}\)
\(Q=\{3,6,9,12,15,18\}\)
\(R=\{4,8,12,16\}\)
\(P\cup Q \cup R=\{1,2,3,4,6,8,9,12,15,16,18,24\}\) |
Draw a Venn diagram to represent sets \(P\), \(Q\) and \(R\), and shade the regions that represent \(P \cup Q\) and \(P\cup Q \cup R\).
| \(P \cup Q\) |
 |
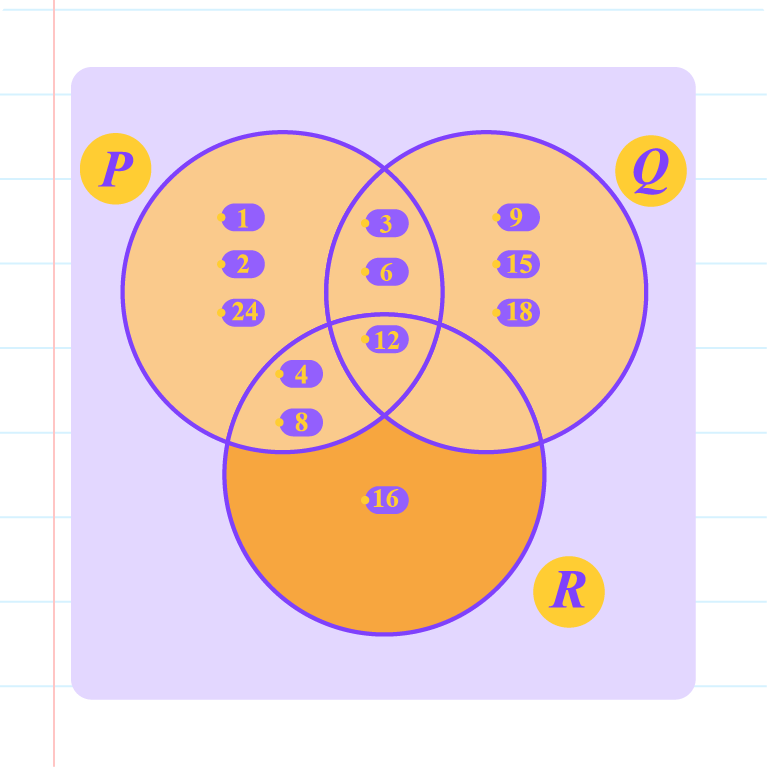| \(P \cup Q\cup R\) |
 |
|
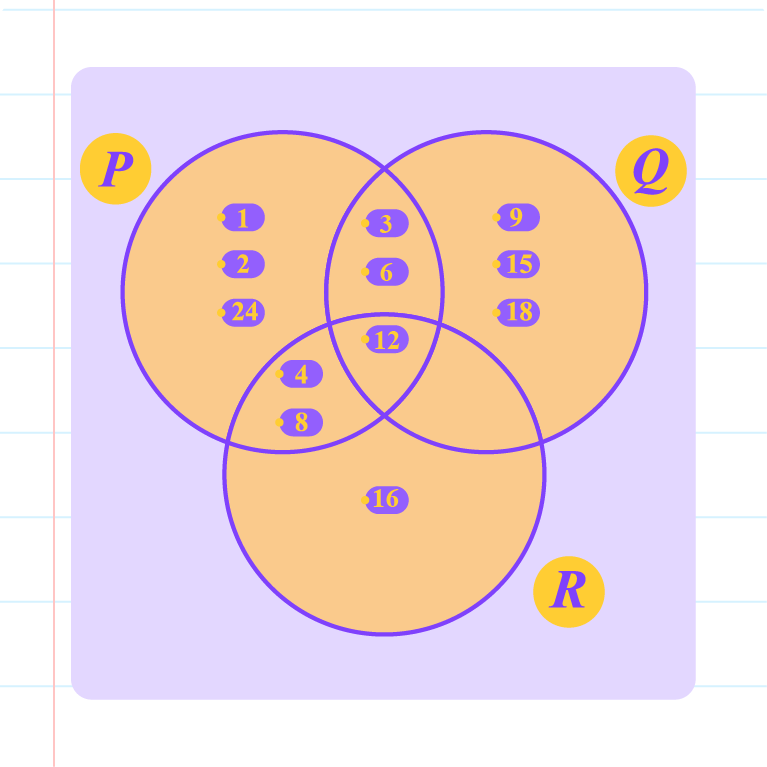| The Complement of The Union of Sets |
- It is written as \((A \cup B)'\).
- \((A \cup B)'\) read as " the complement of the union of sets of sets \(A\) and \(B\) ".
- \((A \cup B)'\) refers to all the elements not in set \(A\) and set \(B\).
|
|
Given the universal set, \(\xi=\{x:x\text{ is an integer},50\le x\le60\}\), set \(G=\{x:x\text{ is a prime number}\}\), set \(H=\{x:x\text{ is a multiple of 4}\}\) and set \(I=\{x:x\text{ is a multiple of 5}\}\), list all the elements and state the number of \((G\,\cup H)'\), \((G\,\cup I)'\), \((H\,\cup I)'\) and \((G\,\cup H\,\cup I)'\).
Solution:
\(\xi=\{50,51,52,53,54,55,56,57,58,59,60\}\)
\(G=\{53,59\}\)
\(H=\{52,56,60\}\)
\(I=\{50,55,60\}\)
| \(n(G\,\cup H)'\) |
\((G\,\cup H)=\{52,53,56,59,60\}\)
\((G\,\cup H)'=\{50,51,54,55,57,58\}\)
\(n(G\,\cup H)'=6\) |
| \(n(G\,\cup I)'\) |
\((G\,\cup I)=\{50,53,55,59,60\}\)
\((G\,\cup I)'=\{51,52,54,56,57,58\}\)
\(n(G\,\cup I)'=6\) |
| \(n(H\,\cup I)'\) |
\((H\,\cup I)=\{50,52,55,56,60\}\)
\((H\,\cup I)'=\{51,53,54,57,58,59\}\)
\(n(H\,\cup I)'=6\) |
| \(n(G\,\cup H\,\cup I)'\) |
\((G\,\cup H\,\cup I)=\{50,52,53,55,56,59,60\}\)
\((G\,\cup H\,\cup I)'=\{51,54,57,58\}\)
\(n(G\,\cup H\,\cup I)'=4\) |
|
| The Complements of The Unions of Two or More Sets Using Venn Diagrams |
 |
|
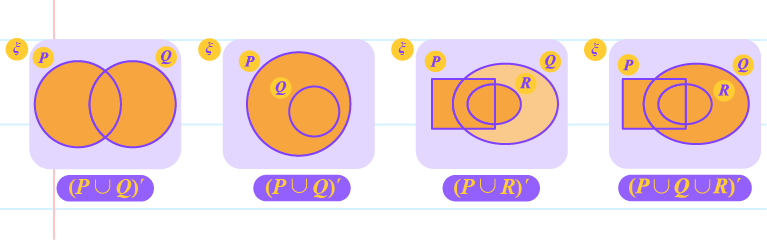Three private travel agencies, \(A,B\) and  \(C\) are chosen to organise the tourism exhibitions \(2020\) in Sarawak. Several divisions in Sarawak are chosen to hold the exhibition as follows:
\(\begin{aligned} \xi= \{&\text{Kapit}, \text{Miri}, \text{Bintulu},\text{Sibu}, \text{Limbang}, \text{Mukah}, \text{Kuching}, \text{Betong} \} \end{aligned}\)
\(\begin{aligned} A=\{&\text{Miri}, \text{Sibu}, \text{Kuching}, \text{Betong}\} \end{aligned}\)
\(\begin{aligned} B=\{&\text{Miri}, \text{Sibu}, \text{Kapit}, \text{Limbang}\} \end{aligned}\)
\(\begin{aligned} C=\{&\text{Miri}, \text{Betong}, \text{Kapit}, \text{Mukah}\} \end{aligned}\)
List all the elements and draw a Venn diagram to represent sets \(A\), \(B\) and \(C\), and shade the region that represents each of \(( A \cup B) '\), \(( B \cup C) '\) and \(( A \cup B \,\cup C) '\).
Solution:
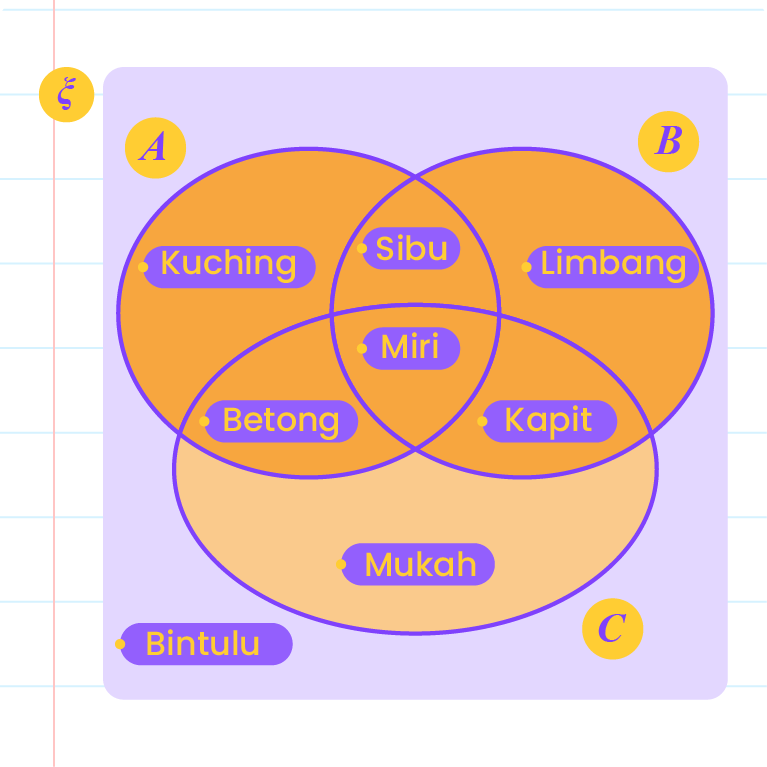
| \(( A \cup B) '\) |
\(A\,\cup B=\{\text{Kapit, Miri, Sibu, Limbang, Kuching, Betong\}}\)
\((A\,\cup B)'=\{\text{Mukah, Bintulu\}}\) |
 |
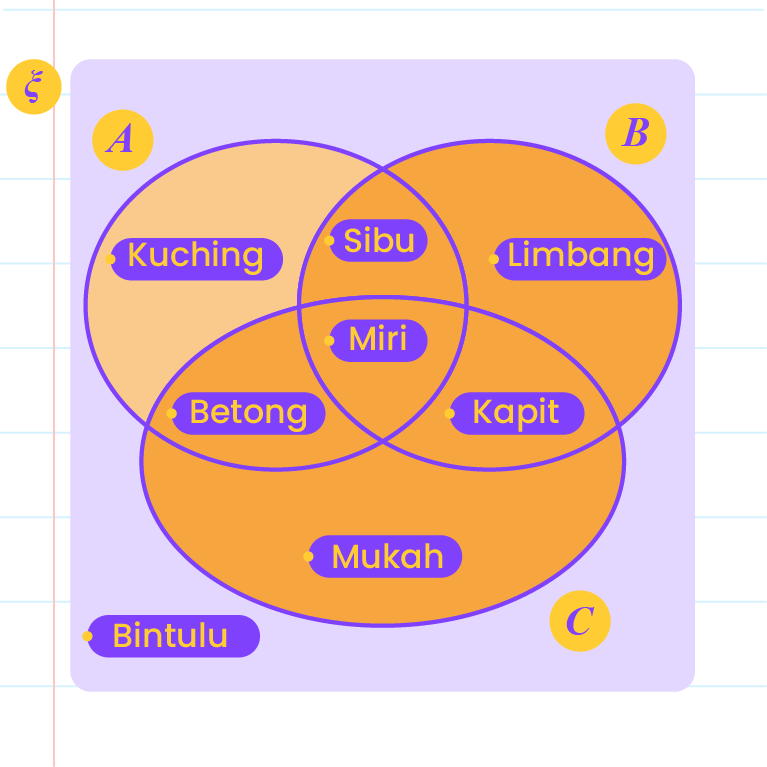
| \(( B \cup C) '\) |
\(B\,\cup C=\{\text{Kapit, Miri, Sibu, Limbang, Betong, Mukah\}}\)
\((B\,\cup C)'=\{\text{Kuching, Bintulu\}}\) |
 |
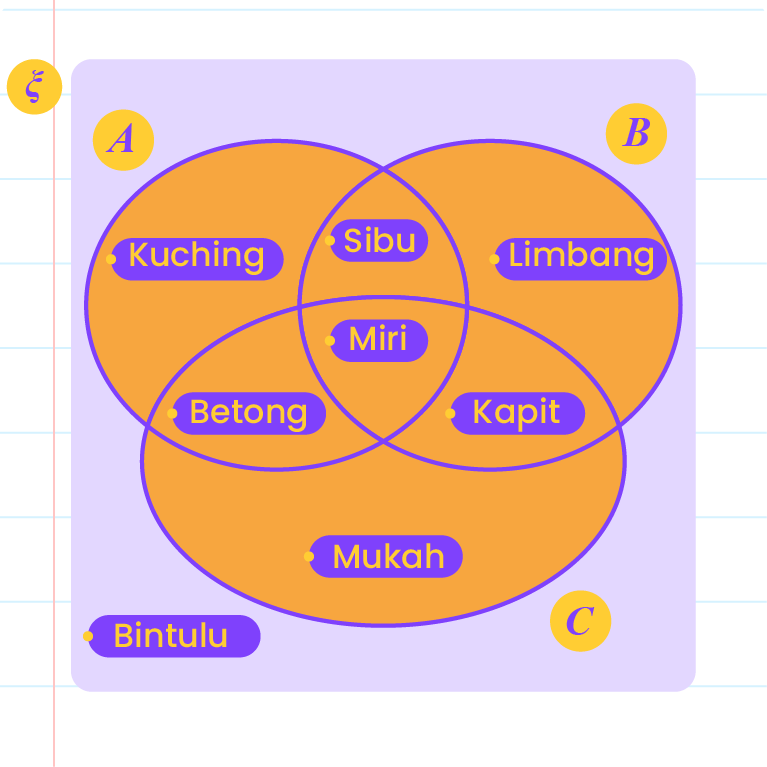
| \(( A \cup B \,\cup C) '\) |
\(A\cup B\,\cup C=\{\text{Kapit, Miri, Sibu, Limbang, Mukah, Betong, Kuching\}}\)
\(( A \cup B \,\cup C) '=\{\text{Bintulu}\}\) |
 |
|
|
