|
Kebolehjadian
Kebolehjadian merujuk kepada kemungkinan suatu peristiwa berlaku. Kebolehjadian juga disebut sebagai kebarangkalian. Kaedah hafalan mungkin menjadi norma kebiasaan dalam memahami konsep kebolehjadian. Terdapat lima kebolehjadian peristiwa iaitu mustahil, kecil kemungkinan, sama kemungkinan, besar kemungkinan, dan pasti.
Terdapat beberapa kaedah yang menarik boleh diguna pakai oleh guru dalam membantu murid memahami topik kebarangkalian yang boleh dianggap baru pada murid – murid sekolah rendah.
|
Kebolehjadian
|
Definisi
|
|
Mustahil
|
Peristiwa yang tidak mungkin berlaku.
|
|
Kecil kemungkinan
|
Kemungkinan sesuatu perkara berlaku itu kecil.
|
|
Sama kemungkinan
|
Sesuatu peristiwa itu mungkin berlaku atau mungkin tidak berlaku.
|
|
Besar kemungkinan
|
Kemungkinan sesuatu peristiwa itu berlaku adalah lebih besar.
|
|
Pasti
|
Peristiwa yang akan terjadi.
|
| |
|
|
Rajah 1: Lima kebolehjadian peristiwa
|
Di sini dikongsikan kaedah yang boleh membantu murid untuk memahami kebolehjadian dengan lebih menarik iaitu dengan menggunakan garis nombor.
Memahami Kebolehjadian Menerusi Garis Nombor
Langkah pertama menggunakan garis nombor bagi memahami kebolehjadian adalah dengan membina garis nombor terlebih dahulu.
|
Rajah 2: Garis nombor
|
Guru perlu membimbing murid untuk memahami simbolik garis nombor yang disuaipadankan dengan kebolehjadian. Memandangkan terdapat kebolehjadian sesuatu peristiwa ada lima, apabila disuaipadankan dengan garis nombor, digit 0 hingga 4 digunakan.
|
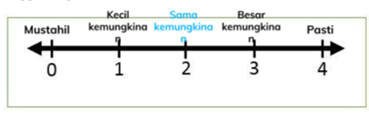
Rajah 3: Suaipadanan garis nombor dengan kebolehjadian
|
1. Kebolehjadian MUSTAHIL dan PASTI
Kebolehjadian mustahil disuaipadankan dengan 0. Terangkan kepada murid bahawa digit 0 disimbolikkan dengan ‘mustahil’. Manakala digit 4 disuaipadankan dengan kebolehjadian ‘pasti’.
2. Kebolehjadian SAMA KEMUNGKINAN
Kebolehjadian sama kemungkinan disuaipadankan dengan 2. Terangkan kepaa murid bahawa 2 adalah di tengah – tengah, di antara 0 (mustahil) dengan 4 (pasti).
3. Kebolehjadian KECIL KEMUNGKINAN dan BESAR KEMUNGKINAN
Kebolehjadian kecil kemungkinan disuaipadankan dengan 1. Terangkan kepada murid bahawa 1 adalah di tengah – tengah, di antara 0 (mustahil) dengan 2 (sama kemungkinan). Begitu juga besar kemungkinan, disuaipadankan dengan 3. Terangkan kepada murid bahawa 3 adalah di tengah – tengah di antara 2 (sama kemungkinan) dengan 4 (pasti)
Secara amnya, guru menunjukkan garis nombor yang disuaipadankan kebarangkalian peristiwa kepada dan menerangkan dengan mengunakan kontekstual. Gunakan laras bahasa yang rendah bagi menerangkan suaipadanan ini kepada murid. Bimbing murid memahami konsep kebarangkalian dengan menggunakan garis nombor.
|
 Login
Login My Account
My Account










