|
Dalam kelas Matematik, berfikir selalunya berkait dengan proses penyelesaian masalah. Kebolehan dalam menyelesaikan sesuatu masalah Matematik bergantung dengan tahap pemikiran seseorang pelajar.
Penyelesaian masalah akan menunjukkan perhubungan antara fakta, konsep atau teorem dalam dalam Matematik; algoritma dan masalah dalam kehidupan seharian. Prosedur atau algoritma perlulah dibezakan dengan kemahiran menyelesaikan masalah dalam Matematik.
Algoritma ialah suatu model, cara atau teknik yang digunakan untuk menyelesaikan sesuatu masalah Matematik. Contohnya, untuk menyelesaikan masalah mencari isi padu sebuah kuboid, algoritma yang digunakan ialah:
Kemahiran menyelesaikan masalah dalam Matematik merupakan satu proses yang agak mencabar yang terdiri daripada langkah-langkah yang mungkin berulang-alik. Ramai pakar Matematik telah menghasilkan heuristik dan pelajar seharusnya menggunakannya sebagai panduan untuk menyelesaikan masalah Matematik.
Gambar Rajah 1 menunjukkan satu model untuk menyelesaikan masalah dalam pembelajaran Matematik. Kita perlulah ingat bahawa langkah-langkah tersebut berulang-alik semasa proses penyelesaian masalah.
|
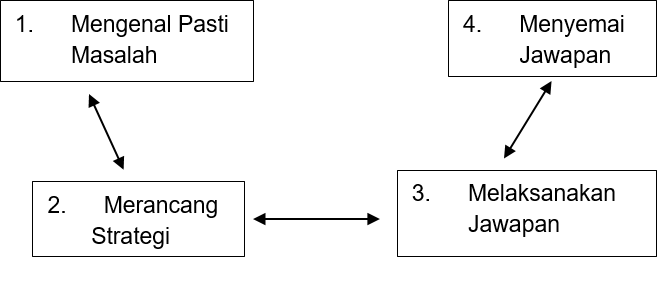
Gambar Rajah 1: Model Penyelesaian Masalah
|
MENGENAL PASTI MASALAH
Pelajar perlu memahami sesuatu masalah Matematik dengan membaca, mengecam fakta, dan menentukan apa yang hendak dicari atau dibukti. Pelajar juga perlu menelitikan maklumat, syarat yang diberikan dalam masalah itu dan mengaitkan dengan contoh yang telah dipelajari.
Contoh:
Apakah yang dikehendaki? Isi padu kuboid
Apakah maklumat yang diberi? Kuboid itu mempunyai panjang 5 cm, lebar 3 cm dan tinggi 14 cm
MERANCANG STRATEGI MENYELESAIKAN MASALAH
Antara kemahiran berfikir dalam merancang strategi adalah seperti berikut:
- Menyusun fakta atau data
- Mengelaskan
- Mengingat kembali konsep
- Teorem
- Formula
- Membuat gambar rajah
- Lakaran
- Jadual
- Mencari kesemua cara alternatif
- Menginterpretasi
- Mengecam perhubungan
- Mengecam pola.
Contoh:
Cari isi padu pepejal yang dijanakan dengan mengisarkan rantau antara parabola \(x =y^2 + 1\) dan garis \(x=3\) pada garis \(x=3 \).
Apakah kehendak soalan? Mencari isi padu pepejal yang dijanakan.
Apakah strategi penyelesaian? Isi padu dapat dicari dengan melukis gambar rajah dan menggunakan rumus.
MELAKSANAKAN JAWAPAN MENYELESAIKAN MASALAH
Langkah ini melibatkan kemahiran berfikir seperti membuat anggaran, melaksanakan operasi kiraan, menggunakan kemahiran algebra, menggunakan kemahiran geometri, mendapat jawapan alternatif, dan sebagainya.
Contoh:
Sebuah bekas berbentuk silinder mengandungi tiga biji bola. Berapakah pecahan isi padu dalam bekas itu yang telah diisi dengan bola? (Andaikan jejari silinder = jejari sfera)
Melaksanakan strategi:
MENYEMAK JAWAPAN
Pelajar harus menyemak jawapannya untuk menentukan sama ada jawapan itu telah mencapai matlamat terhadap masalah itu, dan tidak jauh daripada anggaran yang telah dibuat. Langkah ini melibatkan kemahiran berfikir menyemak langkah-langkah penyelesaian yang telah dilakukan, memperoleh penyelesaian melalui strategi yang lain, dan menggunakan proses songsangan atau penggantian.
Contoh:
(Contoh daripada sebelumnya)
Oleh sebab \(4\pi j^3 = a \pi j^2t\) ------------- (1)
Gantikan \(a = \frac{4j}{t}\) ke dalam persamaan (2)
\(4\pi j^3 = \frac{(4j)\pi j^2t}{t}\)
Maka, \(4 \pi j^3 = 4 \pi j^3 \)
Di sebelah kiri = Di sebelah kanan
|
 Login
Login My Account
My Account










