|
THE VARIATION THEORY OF LEARNING
The variation theory of learning was derived from the phenomenography tradition where variation theory posits that learning implies seeing or experiencing critical aspects of an objects of learning (Marton, 2015; Marton & Booth, 1997).
As stated by Bussey, Orgill and Crippen (2013, p. 9), “…how is it that two students who are sitting in that same class on the same day with access to the same materials can come to understand any concept differently?”. Pupils’ individual perceptions of certain critical features based on their experienced variation within and between features allows them to construct a mental model of a given concept that is unique to them.
ROTATING 2-D SHAPES
Let say pupil is learning about characteristics of a right-angled triangle. Teacher then shows a series of right-angled triangle with different rotation. The intended object of learning is the characteristic of a right-angled triangle.
The characteristic of the right-angled triangle is remaining constant while the position of the right-angled triangles being posed are varied. By doing this, teacher can direct pupils’ attention to the main characteristics of a right-angle triangle as the object of learning. Thus, teacher can guide pupil to discern the characteristic of right-angled triangle, noting that the characteristic of the right-angled triangle remains the same even though the right-angled triangle being rotated into many variations.
|

Diagram 2: Rotated right-angled triangles are still right-angled triangle
|
Diagram 2 shows that even though a right-angled triangle being rotated, the characteristic posit by the right-angled triangle remains the same. This implies the variation theory of learning where pupils, as long as teacher is able to guide pupil with the important characteristics of a right-angle triangle, pupil can identify the right-angle triangle no matter its position, rotation or location.
USING DIFFERENT COLOUR AND SIZE IN VARIATION
Other than rotation, by using different colour also implies the variation theory of learning. Pupils can have individual perceptions of certain critical features based on their experienced variation within and between features allows them to construct a mental model of a given concept that is unique to them.
|
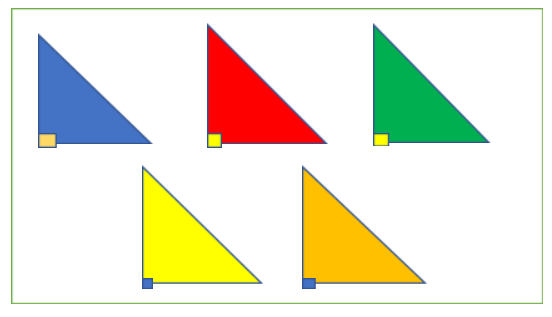
Diagram 3: Even in different colours, the characteristic of right-angled triangles is remaining the same.
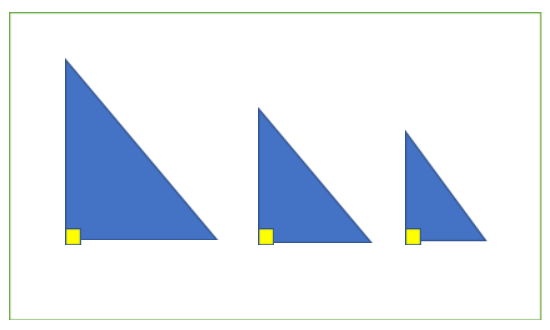
Diagram 4: Also in different sizes, the characteristic of right-angled triangles is remaining the same.
|
Reference:
- Marton, F. (2015). Necessary conditions of learning. New York: Routledge.
- Marton, F., & Booth, S. (1997). Learning and awareness. Mahwah N.J.: Lawrence Erlbaum.
|
 Login
Login My Account
My Account









