SULIT
|
|

|
JABATAN PEPERIKSAAN
PANDAI EDUCATION
|

|
SIJIL PELAJARAN MALAYSIA 2024
|

|
MATEMATIK TAMBAHAN
Kertas 2 (Set 1)
3472/2
|
 |
|
|
 |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 1. |
| (a) |
\(a=18\) cm, \(r=0.8\) |
| |
\(18(0.8)^9\) |
| |
\(2.4159\) cm |
|
1m
1m
1m
|
7m |
| (b) |
\(18(0.8)^{n-1}\lt 2\) |
| |
\((n-1)\lg{(0.8)}\lt \lg{\left(\dfrac{1}{9}\right)}\) |
| |
\(n=11\) |
|
1m
1m
|
| (c) |
\(\dfrac{18}{1-0.8}\) |
| |
\(90\) cm |
|
1m
1m
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 2. |
| (a) |
(i) |
\(m_{UT}=\dfrac{2}{5}\), \(m_{UV}=-\dfrac{5}{2}\) |
| |
|
\(\dfrac{q-6}{p-5}=-\dfrac{5}{2}\) |
| |
|
\(p=\dfrac{37-2q}{5}\) |
| |
|
|
| |
(ii) |
\(\begin{aligned} \triangle{TUV}&=\dfrac{1}{2}|(5q+4p)-(20+6p)|\\ &=p-\dfrac{5}{2}q+10 \end{aligned}\) |
|
1m
1m
1m
1m
|
6m |
| (b) |
\(p-\dfrac{5}{2}q+10=29\) |
| |
\(\dfrac{37-2q}{5}-\dfrac{5}{2}q+10=29\) |
| |
\(V(9,-4)\) |
|
1m
1m
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 3. |
| (a) |
(i) |
\((x-\alpha)(x-\beta)=0\) DAN |
| |
|
\(x^2-(\alpha+\beta)x+\alpha\beta=0\) ATAU \(x^2+\left(\dfrac{b}{a}\right)x+\dfrac{c}{a}=0\) |
| |
|
Guna \(\alpha +\beta =-\dfrac{b}{a}\) DAN \(\alpha\beta=\dfrac{c}{a}\) |
| |
|
|
| |
(ii) |
\(SOR=\dfrac{15}{2}\), \(POR=-3\) |
|
1m
1m
2m
|
7m |
| (b) |
\(4x^2-6x-23=0\) |
| |
\(\dfrac{-(-6)\pm\sqrt{(-6)^2-4(4)(-23)}}{2(4)}\) |
| |
\(\dfrac{3\pm\sqrt{101}}{4}\) |
|
1m
1m
1m
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 4. |
| (a) |
\(\dfrac{dy}{dx}=3x^2-12\), \(m=15\) |
| |
\(y+9=15(x-3)\) |
| |
\(y=15x-54\) |
|
1m
1m
1m
|
7m |
| (b) |
\(P=y^2-12y+16\) ATAU setara |
| |
\(\dfrac{dP}{dy}=2y-12\) |
| |
\(P=(6)^2-12(6)+16\) |
| |
\(-20\) |
|
1m
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 5. |
| (a) |
(i) |
\(\log_2{\left(\dfrac{2\times3^2}{5}\right)}\) |
| |
|
\(1+2h-k\) |
| |
|
|
| |
(ii) |
\(\log_2{(3^2\times2\times5)}\) |
| |
|
\(1+k+3h\) |
|
1m
1m
1m
1m
|
7m |
| (b) |
\(\dfrac{8+\sqrt{24}}{\sqrt{2}+\sqrt{8}}\times\dfrac{\sqrt{2}-\sqrt{8}}{\sqrt{2}-\sqrt{8}}\) ATAU setara |
| |
\(\dfrac{8\sqrt{2}-8\sqrt{8}+\sqrt{48}-\sqrt{192}}{2-\sqrt{16}+\sqrt{16}-8}\) ATAU setara |
| |
\(\dfrac{4\sqrt{2}+2\sqrt{3}}{3}\) |
|
1m
1m
1m
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 6. |
|
(a)
|
\(\begin{aligned} \cos{2x}&=\cos^2{x}-\sin^2{x} \\ &=(1-\sin^2{x})-\sin^2{x} \\ &=1-2\sin^2{x} \end{aligned}\) ATAU \(\begin{aligned} &=(\sin^2{x}+\cos^2{x})-2\sin^2{x}\\ &=\cos^2{x}-\sin^2{x} \\ &=\cos{2x} \end{aligned}\) |
|
1m
1m
|
6m |
| (b) |
(i) |
\(y=\cos{2x}\) |
| |
|
|
| |
(ii) |
|
| |
|
|
| |
|
Bentuk |
| |
|
Graf dipantulkan atas paksi-\(x\) |
| |
|
Bilangan penyelesaian: \(4\) |
|
1m
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 7. |
| (a) |
\(\pi r^2h=81\pi\) |
| |
\(L=\pi r(2r)+2\pi r\left(\dfrac{81}{r^2}\right)+\pi r^2\) |
| |
\(L=3\pi \left(r^2+\dfrac{54}{r}\right)\) |
|
1m
1m
1m
|
10m |
| (a) |
Bezakan \(L\) terhadap \(r\), |
| |
\(\dfrac{dL}{dr}=3\pi \left(2r-\dfrac{54}{r^2}\right)\) |
| |
Samakan \(\dfrac{dL}{dr}\) dengan \(0\) & selesaikan untuk \(r\), |
| |
\(3\pi \left(2r-\dfrac{54}{r^2}\right)=0\) |
| |
\(81\pi\) |
|
1m
1m
1m
|
| (c) |
\(\dfrac{dr}{dt}=\dfrac{1}{3\pi\left(2(6)-\dfrac{54}{(6)^2}\right)}\times63\pi\) |
| |
\(2\) |
|
1m
1m
|
| (d) |
\(\dfrac{dL}{dr}=(6.002-6)\times\dfrac{63}{2}\pi\) |
| |
\(0.063\pi\) |
|
1m
1m
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 8. |
| (a) |
(i) |
\(0=27-(x-2)^3\) |
| |
|
\(-27=-(x-2)^3\) |
| |
|
\(3^3=(x-2)^3\) |
| |
|
\(x=5\) koordinat \((5,0)\) |
| |
|
|
| |
(ii) |
\(\int_0^5 27-(x-2)^3\ dx\) |
| |
|
\(\left[ 27x-\dfrac{(x-2)^4}{4} \right]_0^5\) |
| |
|
\(\left[ 27(5)-\dfrac{((5)-2)^4}{4} \right]_0^5-0\) |
| |
|
\(115.25\) unit\(^2\) |
|
1m
1m
1m
1m
1m
1m
|
10m |
| (b) |
\(\pi\int_k^4 (\sqrt{3x+4})^2 \ dx=\pi\int_k^43x+4\ dx=26\pi\) |
| |
\(\pi\left[ \dfrac{3x^2}{2}+4x\right]_k^4=26\pi\) |
| |
\(\left[\dfrac{3(4)^2}{2}+4(4)\right]-\left[\dfrac{3(k)^2}{2}+4(k)\right]=26\) |
| |
\(-3k^2-8k+28=0\) |
| |
\(k=2\) |
|
1m
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 9. |
| (a) |
\(\sin{x}\cos{\left(\dfrac{\pi}{6}\right)}+\cos{x}\sin{\left(\dfrac{\pi}{6}\right)}-\left( \sin{x}\cos{\left(\dfrac{\pi}{6}\right)}-\cos{x}\sin{\left(\dfrac{\pi}{6}\right)} \right)\) |
| |
\(2\cos{x}\sin{\left( \dfrac{\pi}{6}\right)}\) |
| |
\(2\cos{x}\left(\dfrac{1}{2}\right)\) |
| |
\(\cos{x}\) |
|
1m
1m
|
10m |
| (b) |
| \(x\) |
\(0\) |
\(\dfrac{\pi}{4}\) |
\(\dfrac{\pi}{2}\) |
\(\dfrac{3\pi}{4}\) |
\(\pi\) |
| \(y\) |
\(5\) |
\(2\) |
\(-1\) |
\(2\) |
\(5\) |
|
| |
\(y=\dfrac{8x}{\pi}+1\) |
| |
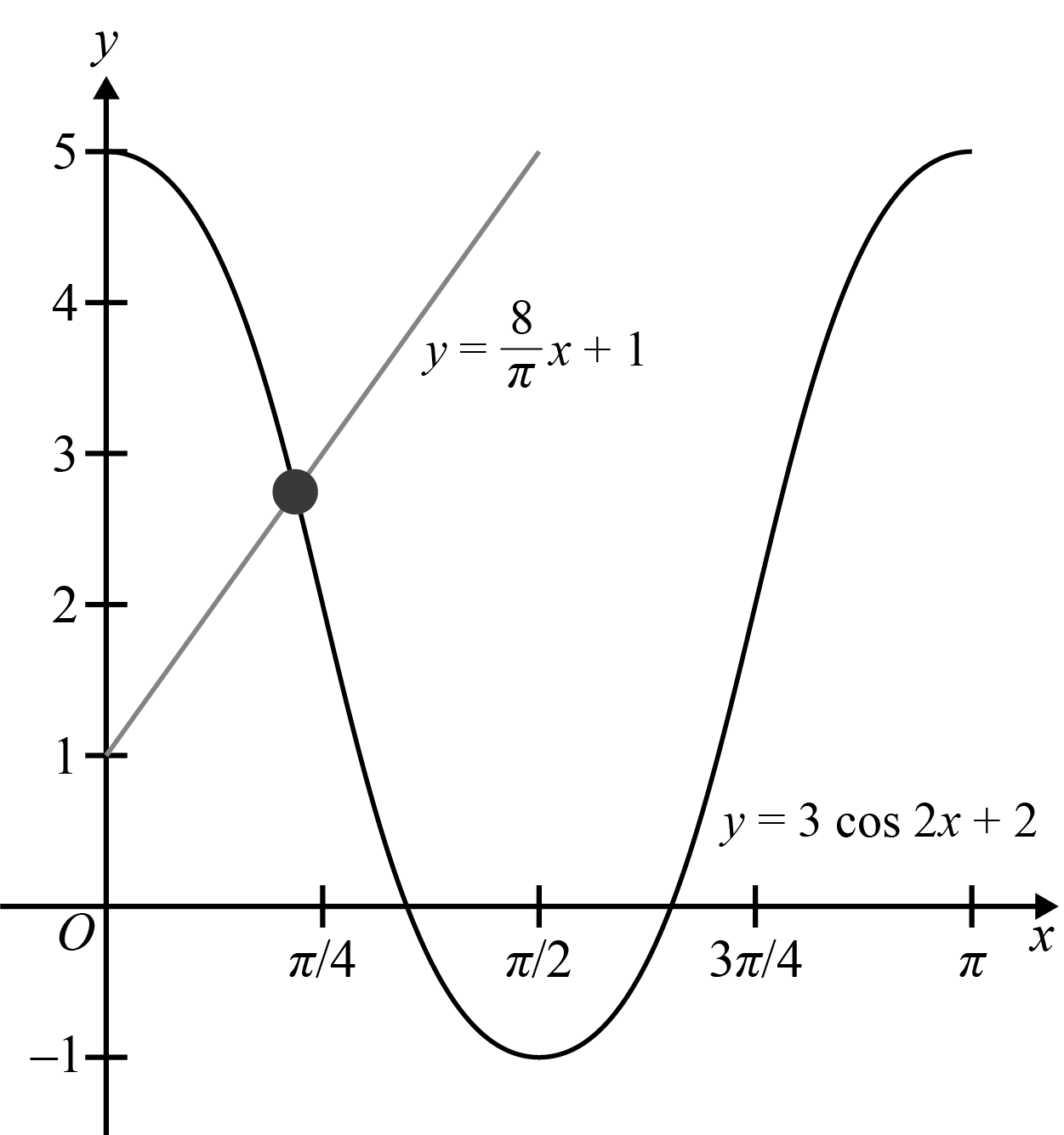 |
- Bentuk kos
- Titik maksimum / minimum
- Kitaran atau pusingan / anjakan
|
|
| |
\(1\) penyelesaian |
|
1m
1m
1m
1m
1m
|
| (c) |
\(\cos{x}(2\sin{x}+1)=0\) |
| |
\(\cos{x}=0\), \(2\sin{x}+1=0\) |
| |
\(x=90^\circ\), \(x=270^\circ\) |
| |
\(x=180^\circ+30^\circ\), \(x=360^\circ-30^\circ\) |
|
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 10. |
| (a) |
| \(x\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(6\) |
\(7\) |
| \(\log_{10}{y}\) |
\(1.75\) |
\(1.48\) |
\(1.40\) |
\(0.95\) |
\(0.80\) |
\(0.53\) |
\(0.25\) |
|
| |
Kesemua titik bagi \(\log_{10}{y}\) betul
|
| |
|
| |
Satu titik betul |
| |
Semua titik betul |
| |
Garis penyuaian terbaik |
|
1m
1m
1m
1m
|
10m |
| (b) |
(i) |
\(y_\text{salah}=25.1\) ; \(y_\text{betul}=17.78\) |
| |
|
|
| |
(ii) |
\(\log_{10}{y}=-(\log_{10}n)x+\log_{10}m\) |
| |
|
\(-\log_{10}n=\) kecerunan |
| |
|
\(n=1.778\) |
| |
|
\(\log_{10}m=2\) |
| |
|
\(m=100\) |
|
1m
1m
1m
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 11. |
| (a) |
(i) |
\(n(0.2)=50\) |
| |
|
\(n=250\) |
| |
|
|
| |
(ii) |
\({}^{10}C_4(0.2)^4(0.8)^6\) |
| |
|
\(=0.08808\) |
|
1m
1m
1m
1m
|
10m |
| (b) |
(i) |
\(\mu=3.1\), \(\sigma^2=0.09\), \(\sigma=0.3\) |
| |
|
\(\begin{aligned} P(2.9\lt Z\lt 3.1)&=P\left(\dfrac{2.9-3.1}{0.3}\lt Z\lt \dfrac{3.3-.31}{0.3}\right) \\ &=P\left(-\dfrac{2}{3}\lt Z\lt \dfrac{2}{3}\right)\\ &=0.4950 \end{aligned}\) |
| |
|
|
| |
(ii) |
\(P(X\lt m)=0.25\) |
| |
|
\(P\left(Z\lt \dfrac{m-3.1}{0.3}\right)=0.25\) |
| |
|
\(\dfrac{m-3.1}{0.3}=-0.674\) |
| |
|
\(m=3.1-0.674(0.3)\) |
| |
|
\(m=2.898\) kg |
|
1m
1m
1m
1m
1m
1m
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 12. |
| (a) |
\(q=\dfrac{100}{80}\times 100\) |
| |
\(q=125\) |
|
1m
1m
|
10m |
| (b) |
(i) |
\(\left(\dfrac{110}{100}\times125\right)\) ATAU \(\left(\dfrac{110}{100}\times140\right)\) |
| |
|
\(137.5\) DAN \(154\) |
| |
|
|
| |
(ii) |
\(\dfrac{137.5(2p)+121(6)+112(3)+154(p)}{2p+6+3+p}=128\) |
| |
|
\(p=2\) |
|
1m
1m
2m
1m
|
| (c) |
(i) |
Komponen Membeli-belah kerana mempunyai nilai pemberat paling besar. |
| |
|
|
| |
(ii) |
\(\dfrac{151.25}{121}\times100=125\%\) |
| |
|
Peratus peningkatan \(=25\%\) |
|
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 13. |
| (a) |
Titik \(C\) |
| |
\(AC\) adalah garis terpanjang kerana sudut bertentangannya adalah sudut terbesar bagi kedua-dua segi tiga \(ABC\) dan \(ADC\). |
|
1m |
10m |
| (b) |
(i) |
\(\dfrac{AC}{\sin{93.20^\circ}}=\dfrac{64}{\sin{(180^\circ-93.20^\circ-58^\circ)}}\) |
| |
|
\((^*AC)^2=52.4^2+109^2-2(52.4)(109)\cos{\angle{ADC}}\) |
| |
|
\(105.05^\circ\) ATAU setara |
| |
|
|
| |
(ii) |
\(\dfrac{1}{2}(52.4)(109)\sin(^*105.05^\circ)\) |
| |
|
ATAU |
| |
|
\(\dfrac{1}{2}(64)(^*132.64)\sin(58^\circ)\) |
| |
|
\(\dfrac{1}{2}(52.4)(109)\sin(^*105.05^\circ)+\dfrac{1}{2}(64)(^*132.64)\sin(58^\circ)\) |
| |
|
\(6357.37\) |
|
1m
1m
1m
1m
1m
1m
|
| (c) |
(i) |
|
| |
|
|
| |
|
|
| |
(ii) |
\(\dfrac{1}{2}\times AE\times 109=^*2757.84\) |
| |
|
\(50.60\) |
|
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 14. |
| (a) |
\(\text{I}:45x+30y\le 330\) |
| |
\(\text{II}:50x+70y\ge 350\) |
| |
\(\text{III}:y\ge\dfrac{5}{4}x\) |
|
1m
1m
1m
|
10m |
| (b) |
|
| |
|
| |
Lukis sekurang-kurangnya satu garis lurus dengan betul |
| |
Lukis semua garis lurus dengan betul |
| |
Lorek rantau dengan betul |
|
1m
1m
1m
|
| (c) |
(i) |
\(4\le y\le 6\) |
| |
|
|
| |
(ii) |
\((4,5)\) |
| |
|
\(16(4)+10(5)\) |
| |
|
RM \(114\) |
|
1m
1m
1m
1m
|
|
| |
|
|
|
|
| |
| |
Skema Jawapan |
Sub Markah |
Jumlah Markah |
| 15. |
| (a) |
(i) |
Ganti dan samakan dengan \(4\), |
| |
|
\(2(6)-p=4\) |
| |
|
\(p=8\) |
| |
|
|
| |
(ii) |
\((t-3)(t-5)=0\) |
| |
|
\(t=3\), \(t=5\) |
|
1m
1m
1m
1m
|
10m |
| (b) |
|
| |
|
| |
Bentuk |
| |
Titik persilangan \((0,15)\), \((3,0)\) dan \((5,0)\) |
| |
|
| |
Kamir dengan had yang betul, |
| |
\(\int_0^3t^2-8t+15\ dt\) ATAU \(\int_3^5t^2-8t+15\ dt\) |
| |
\(\left[ \dfrac{t^3}{3}-\dfrac{8t^2}{2}+15t \right]_0^3\) ATAU \(\left[ \dfrac{t^3}{3}-\dfrac{8t^2}{2}+15t \right]_3^5\) |
| |
Gunakan nilai had yang betul, |
| |
\(\left[ \dfrac{(3)^3}{3}-\dfrac{8(3)^2}{2}+15(3) \right]-\left[ \dfrac{(0)^3}{3}-\dfrac{8(0)^2}{2}+15(0) \right]\) |
| |
ATAU |
| |
\(\left[ \dfrac{(5)^3}{3}-\dfrac{8(5)^2}{2}+15(5) \right]-\left[ \dfrac{(3)^3}{3}-\dfrac{8(3)^2}{2}+15(3) \right]\) |
| |
\(18+\left| -\dfrac{4}{3} \right|\) |
| |
\(\dfrac{58}{3}\) |
|
1m
1m
1m
1m
1m
1m
|
|
| |