| |
|
|
| |
| Congruent line segments: |
| |
| Definition |
|
Line segments having the same length.
|
|
| |
- A line segment is denoted using capital letters at both ends.
|
| |
| Example |
|
|
|
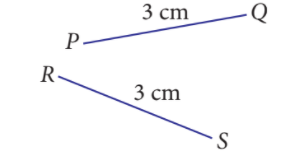
We can see that both line segments, \(PQ\) and \(RS\), have the same length.
Thus, \(PQ\) and \(RS\) are congruent.
|
|
| |
| Congruent angles: |
| |
| Definition |
|
Angles having the same size.
|
|
| |
|
|
| |
| Example |
|
|
|
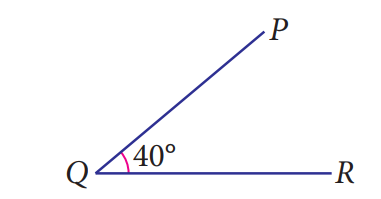
We can see that,
\(\angle PQR=40^\circ\) or \(\angle RQP=40^\circ\).
Thus, \(\angle PQR\) and \(\angle RQP\) are congruent.
|
|
| |
| Estimate and measure the length of a line segment and the size of an angle: |
| |
- An angle that appears more than a right angle has an angle greater than \(90^\circ\).
- An angle that appears less than a right angle has an angle less than \(90^\circ\).
|
| |
|

|
| |
- The size of an angle can be measured more accurately using a protractor.
|
| |
| The properties of the angle on a straight line, a reflex angle and the angle of one whole turn: |
| |
|
The angle on a straight line
- The sum of angles on a straight line is \(180^{\circ}\).
|
| |
|
Reflex angle
|
| |
|
The angle of one whole turn
|
| |
| The properties of complementary angles, supplementary angles and conjugate angles: |
| |
|
Complementary angles
- The sum of the two angles is always \(90^\circ\).
|
| |
|
Supplementary angles
|
| |
|
Conjugate angles
|
| |
| Perform a geometrical construction: |
| |
|
(i) Line segments
- A section of a straight line with a fixed length.
|
| |
| Example |
|
Construct the line segment \(AB\) with a length of \(8\text{ cm}\) using only a pair of compasses and a ruler.
|
|

|
|
| |
|
(ii) Perpendicular bisectors
- If line \(AB\) is perpendicular to line segment \(CD\) and divide \(CD\) into two parts of equal length, then line \(AB\) is known as the perpendicular bisector of \(CD\).
|
| |
| Example |
|
Construct the perpendicular bisector of line segment \(PQ\) using only a pair of compasses and a ruler.
|
|

|
|
| |
|
(iii) Perpendicular line to straight line
- If a line is perpendicular to line \(PQ\), then the line is known as perpendicular line to line \(PQ\).
|
| |
| Example |
|
Using only a pair of compasses and a ruler, construct the perpendicular line from point \(M\) to the straight line \(PQ\).
|
|

|
|
| |
|
(iv) Parallel lines
- Lines that will never meet even when they are extended.
|
| |
| Example |
|
Using only a pair of compasses and a ruler, construct the line that is parallel to \(PQ\) passing through point \(R\).
|
|

|
|
| |
| Construct angles and angle bisectors: |
| |
| (i) Constructing an angle of \(60^{\circ}\) |
| |
| Example |
|
Using only a pair of compasses and a ruler, construct line \(PQ\) so that \(\angle PQR=60^\circ\).
|
|

|
|
| |
|
(ii) Angle Bisectors
- A line divides an angle into two equal angles.
|
| |
| Example |
|
Using only a pair of compasses and a ruler, construct the angle bisector of \(\angle PQR\).
|
|

|
|
| |