| |
| 2.1 |
Factors, Prime Factors and Highest Common Factor (HCF) |
|
| |
| Factors |
- A number that divides another number completely.
- The factors of \(12\) are \(1, 2,3,4,6\) and \(12\).
|
|
| |
| Example |
|
Is \(12\) the factor of \(36\)?
|
|
\(36\div 12=3\)
Thus, \(12\) is the factor of \(36\).
|
|
| |
| Prime Factor |
|
Factor that is a prime number.
|
|
| |
| Example |
|
The factors of \(18\) are \(1, 2,3,6,9\) and \(18\).
Between these factors, \(2\) and \(3\) are prime numbers.
Thus, the prime factors of \(18\) are \(2\) and \(3\).
|
|
| |
| Solution Methods |
| |
| Repeated division: |
| |
| Express \(60\) in the form of prime factorisation. |
| |
|
Perform division repeatedly by dividing with the smallest prime number.
Division is continued until the quotient is \(1\).
\(\begin{array}{c} 2\\2\\3\\5 \\\phantom{-} \end{array} \begin{array}{|c} \quad60\quad\\ \hline \quad30\quad\\ \hline \quad15\quad\\ \hline \quad5\quad\\ \hline \quad1\quad\\ \end{array} \begin{array}{c}\end{array}\\\\\)
Thus,
\(60=2\times2\times3\times5\).
|
| |
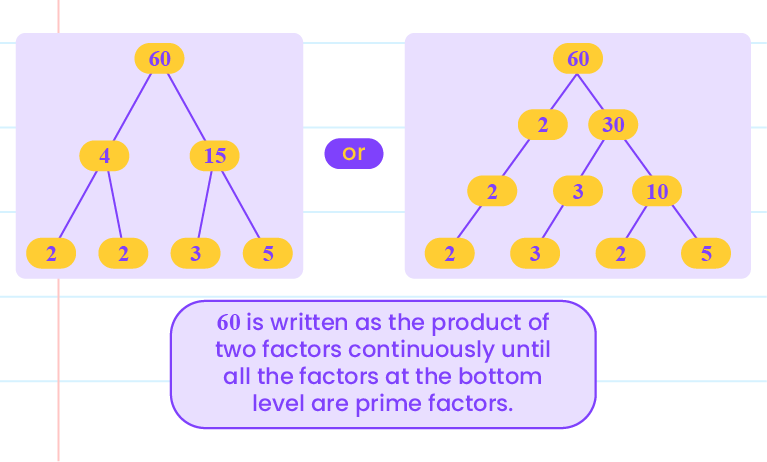
| Factor trees: |
| |
| Express \(60\) in the form of prime factorisation. |
| |
|
|
| |
|
Thus,
\(60=2\times2\times3\times5\).
|
|
| |
| Common Factor |
|
A number that is a factor of a few other numbers.
|
|
| |
| Example |
|
Determine whether \(6\) is a common factor of \(24\) and \(36\).
|
|
\(24\div6=4 \\36\div6=6\)
\(24\) and \(36\) can be divided completely by \(6\).
Thus, \(6\) is a common factor of \(24\) and \(36\).
|
|
| |
| Highest Common Factor (HCF) |
|
The greatest number among the common factors.
|
|
| |
| Example |
|
(i) Determine the highest common factor of \(18\) and \( 24\).
Listing the common factors:
Factors of \(18 : 1 , 2 , 3 , 6 , 9, 18\)
Factors of \(24 : 1 , 2 , 3 , 4 , 6 , 8, 12, 24\)
So, the common factors of \(18 \) and \(24\) is \(1, 2, 3 \) and \(6\).
Thus, HCF is \(6\).
|
|
(ii) Determine the highest common factor of \(30,60\) and \( 72\).
Repeated division:
\(\begin{array}{c} 2\\2\\3 \\\phantom{-} \end{array} \begin{array}{|c} \quad36,\,60,\,72\quad\\ \hline \quad18,\,30,\,36\quad\\ \hline \quad9,\,15,\,18\quad\\ \hline \quad3,\,5,\,6\quad\\ \end{array} \begin{array}{c}\end{array}\\\\\)
Thus, HCF of \(36, 60\) and \(72\) is
\(2\times2\times3 = 12\).
|
|
(iii) Determine the highest common factor of \(48,64\) and \(80\).
Prime factorisation:
\(48 = 2\times2\times 2\times2\times3\)
\(64 = 2 × 2 × 2 × 2 × 2 × 2 \)
\(80 = 2\times2\times 2\times 2\times5\)
Thus, HCF is
\(2 × 2 × 2 × 2 = 16\).
|
|